American Journal of Analytical Chemistry
Vol.09 No.03(2018), Article ID:82805,14 pages
10.4236/ajac.2018.93009
Potentiometric Determination of Stability Constants of Sulphathiazole and Glycine-Metal Complexes
Awad A. Al-Rashdi1*, A. H. Naggar2, O. A. Farghaly2, H. A. Mauof3, A. A. Ekshiba3
1Chemistry Department, Al-Qunfudah Center for Scientific Research (QCSR), Al-Qunfudah University College, Um Al-Qura University, Al-Qunfudah, Saudi Arabia
2Department of Chemistry, Faculty of Science, Al-Azhar University, Assiut, Egypt
3Department of Chemistry, Faculty of Science, Sebha University, Sebha, Libya

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 24, 2017; Accepted: February 27, 2018; Published: March 2, 2018
ABSTRACT
Binary and ternary complexes of (Fe(III), Pb(II), Co(II), Al(III), La(III), Sr(II), Cr(III), Ti(II) and Zr(II)) with sulphathiazole (as primary ligand) and amino acid glycine (as secondary ligand) have been studied potentiometrically at 25˚C ± 0.1˚C and I = 0.1 M NaClO4 in 25% (v/v) pure ethanol-water medium. Although there are many methods available to study the stability of metal-ligand complexes, pH-metry is most frequently used. In extension of our study on solution equilibria, we used Calvin-Bjerrum method for the calculation of stability constants. Stoichiometries and stability constants of binary systems containing the above metal ions in a 1:1 and 1:2 and/or 1:3 ratios were also determined to compare the effect of the secondary ligand on (1:1) Metal:Sulphathiazole system. The protonation constants of the complexes were evaluated for the system M:Sulphathiazole:Glycine = 1:1:1. The order of stability of the binary and ternary complexes was examined. It was found that glycine adds preferably [M-Sulfathiazole] rather than to the aqueous complexes of metal ions. In all cases 1:1:1 complex was formed.
Keywords:
Potentiometry, Glycine, Sulphathiazole, Ternary Complexes

1. Introduction
Sulphonamide drugs have been used clinically since the 1930s in human medicine and livestock production [1] [2] . The medical effect of sulphonamides is to prevent bacterial growth by acting as a competitive inhibitor of dihydropteroate synthase (DHPS) during folate synthesis [3] [4] [5] . The metal chelates of sulphonamides have been found to be more potent bacteriostatic agents than the parent drugs themselves [6] . Sulphathiazole (4-amino-N-(1,3-thiazol-2-yl) benzenesulfonamide, STZ) is one of the first sulfonamides used in humans after sulfa drug discovery, STZ structure is shown below:
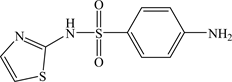
Due to its high toxicity, it is used with other sulfonamides such as sulfabenzamide and sulfacetamide in preparations for the topical treatment of vaginal infections. It is also used in combination with other drugs in the treatment of skin infections [7] [8] . Many metal complexes of STZ are reported in the literature. Some examples are the Co(II)-STZ [9] [10] , Pt(II)-STZ [11] , Hg(II)-STZ [12] , Ag(I)-STZ [13] . Investigation of the binary and ternary complexes of STZ may, therefore, help understand the driving forces leading to the formation of mixed ligand complexes commonly found in biological systems.
The potentiometric method has been used extensively in many branches of solution chemistry. Great attention has been paid to the use of potentiometric methods in the study of binary and ternary complexes of transition metals with molecules of biological and pharmaceutical interest [14] [15] [16] . The importance of potentiometric methods as the most accurate and widely applicable technique in studies related to the ionic equilibrium of different complexes [17] . It should be noted that the presence of metal ions in biological fluids could have a significant effect on the therapeutic action of such organic compounds [18] .
As a continuation of our research into binary and ternary complexes of biological significance [19] [20] [21] , the present article brings a complete potentiometric and conductometric studies on binary and ternary complexes formed between different metal ions (Fe(III), Pb(II), Co(II), Al(III), La(III), Sr(II), Cr(III), Th(IV), Ti(II) and Zr(II)) with sulphathiazole (as primary ligand) and amino acid glycine (as secondary ligand). Potentiometric titrations curves, conductometric titration curves and distribution curves of formed binary and ternary complexes were constructed. The obtained curves were used in calculating stability constants of formed binary and ternary complexes.
2. Experimental
2.1. Apparatus
All the potentiometric measurements were carried out on pH-meter model ELE international, using combined glass electrode (accurate total 0.01 pH units). Conductometric titration measurements were carried out using conductivity meter model 4320, Jenway, using an immersion cell. Before and after each titration, the electrode was calibrated using standard buffer pH ≈ 4.01, pH ≈ 7.00 and pH ≈ 9.00.
2.2. Materials and Methods
All the reagents were of analytical grade. Pure ethanol and bidistilled water were used for the preparation of the solutions. Sulphathiazole (4-amino-N-(1,3-thiazol-2-yl) benzenesulfonamide, STZ) was purchased from Sigma Chemical Company (USA). The salts of metallic nitrates (BDH, U.K, GENEVA or INDIA) will be prepared. The aqueous metal ion solution was standardized according to a well-known method [22] . Standard solutions of 0.1 M sodium hydroxide, 0.01 M perchloric acid and 0.09 M sodium perchlorate in aqueous solutions were prepared as usual. An STZ stock solution (0. 1 M) was prepared by weighing directly in pure ethanol because it is insoluble in water, slightly soluble in ethanol (96%), in chloroform and in ether. The working solutions (0.001 M) were prepared by accurate dilution using the same solvent.
2.3. Procedure
2.3.1. Potentiometric Studies
This is based an the method of Irving and Rossoti equations [23] . For binary and ternary systems, the following solutions were prepared and titrated against 0.1 M of standared CO2-free NaOH solution at 25˚C ± 0.1˚C:
(a) 0.01 M HClO4 + 0.09 M NaClO4.
(b) Solution (a) + 0.001 M STZ.
(c) Solution (b) + 0.001 M metal ion.
(d) Solution (a) + 0.001 M Gly.
(e) Solution (d) + 0.001 M metal ion.
(f) Solution (a) + 0.001 M STZ + 0.001 M Gly + 0.001 M metalion.
In all titrations, the total volume was maintained constant at 50 mL and different ionic strength of NaClO4 in 25% (v/v) aqueous ethanol solution.
2.3.2. Conductometric Studies
It was carried out at room temperature by titrating 25 mL of 0.001 M of each metal ion with 0.01 M of each ligand solution in 0.5 mL increment. Correction for the dilution effect is performed by multiplying the values of specific conductance by a factor (25 + V)/25, where V is the volume of the titrant added.
3. Results and Discussion
3.1. Proton-STZ System
All pH measurements were performed at 25˚C ± 0.1˚C. The medium was aqueous acid and ionic strength 0.1 M NaClO4. For binary complexes studies, three types of mixtures (with total volume 50 mL for each) were used; (a) free acid, (b) STZ (as ligand) and (c) chelate produced from individual reaction of STZ with different metal ions; Ti(II), Zr(IV), Sr(II), Al(III), Cr(III), Fe(III), Th(IV), Pb(II), La(III) and Co(II). As shown in Figure 1, mixtures a, b and c
Figure 1. Representative potentiometric titration curve of STZ at 0.1 M NaClO4 and 25 ± 0.1˚C: (a) 0.01 M HClO4; (b) a + 0.001 M STZ; (c) b + 0.001 M Sr(II); (d) b + 0.001 M Pb(II); (e) b + 0.001 M Co(II); (f) b + 0.001 M Al(III); and (g) b + 0.001 M Fe(III).
were individually titrated against standard alkali and the plots of pH versus volume of alkali gave the titration curves.
(1)
where V2 and V1 are the volumes of alkali required to reach the same pH in acid and ligand titration curves. TcL˚ The total ligand concentration Y is the total number of protons free attached to the ligand molecule, N˚ is the normality of the alkali, E˚ is the initial concentration of the free acid and V0 is the total volume of the titrated solution. The titration curves were used to evaluate (average number of protons associated with STZ); calculations of proton ligand association constants were carried out by plotting a graph of against pH, as we can see in Figure 2. The concentrations were: TcL˚ = 0.001 M, TcM˚ = 0.001 M. From these data, the proton-ligand and metal-ligand stability constants were obtained as in Table 1. The maximum numbers of protons that can be released from STZ are two protons in the titration with diluted base (0.1 M) in the range of pH 2.20 - 11.20. STZ behaves as dibasic acid [H2-STZ]. The acid-base properties of STZ in 25% (v/v) EtOH medium at different ionic strengths of NaClO4 (I =0.1, 0.2, 0.3, 0.4 and 0.5 M) indicate that one proton from the protonated amino group (NH2 → ) was deprotonated in the pH range (3.63 - 4.95).
The ionic strength has an important effect in the electrolytic solutions. It also offers ionic atmosphere, which impacts the stability constant of metal complexes. No precipitates produced, indicating that there was no propensity to form hydroxo complexes as the number of moles of NaOH consumed was equivalent to the number of moles of NaClO4.
It is observed that logka values inversely proportional with the concentration of ionic strength.
The second site is the dissociation of proton in the amino group (NH) in pH range (7.10 - 9.40). The values of and (the first and second
Figure 2. Representative potentiometric constant curves of STZ at 0.1 M NaClO4 and 25 ± 0.1˚C.
proton formation constants of STZ, respectively) are the pH values corresponding to and 1.5, respectively. The values of (7.20) and (3.80) are tabulated in Table 1. However, the reaction mechanism is show as follow:
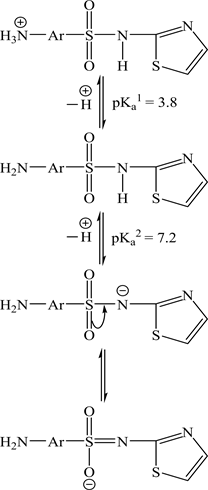
Table 1. Formation constants of STZ and stability constants of metal ion complexes at 0.1 M NaClO4 and 25˚C ± 0.1˚C.
*These ratios are from potentiometric and conductometric methods.
3.2. Binary Metal-STZ Systems
The formation curves of the complexation equilibrium as shown in Figure 3 is obtained by plotting the degree of the complex formation ( ) against the negative logarithm of the concentration of non-protonated ligand (pL) using the Irving and Rossotti equations [23] . From these formation curves, the values of stability constants listed in Table 1 were determined using the half-integral method [23] . The obtained results shows that both Al(III) and Zr(IV) ions forms (1:1), (1:2) and (1:3) metal to ligand complexes. Also, some metal ions viz; Zr(IV), Sr(II), Al(III), Fe(III), Th(IV) and Pb(II) forms (1:1) and (1:2) metal to ligand complexes, but in the case of Co(II), Cr(III), Ti(II) and La(III) only one complex (1:1) metal to ligand was formed. This may be due to the nature of metal ion, concentration of ligand and ionic strength.
(2)
(3)
where Tcm˚ denotes the total concentration of metal present in solution, β is the proton ligand stability constant, the other terms have their usual meaning as mentioned before. The stability constants of the complexes formed with STZ were listed in Table 1 in the order of stability of the different binary complexes formed between STZ and the metal ions investigated in this study, is in the expected Irving-Williams order [23] :
Figure 3. Representative formation curves of binary metal ion complexes with STZ at I = 0.1 MNaClO4: (a) Zr(IV); (b) Ti(II); (c) Sr(II); (d) La(III) and (e) Th(IV).
STZ behavior may be based on the bidentate nature which coordinates through the oxygen atom of sulphonamide group and a sulphur atom in the thiazole ring, forming stable six-membered chelate ring:
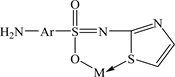
Ratio (1:1) metal: ligand
Also, the study of ionic strength effect on the stability constant of STZ with Al(III), Th(IV), Cr(III), Pb(II) and Zr(IV) metal ions in aqueous solution at 25˚C ± 0.1˚C was discussed. The relation between and the ionic strength is shown in Figure 4. As we can see, the stability constants of metal-ligand complex (1:1) were decreased as the ionic strength increase.
3.3. Conductometric Titration of STZ
The conductometric analysis shows a greater use in tracing the complex formation. This method finds its useful application as a sensitive tool to test for decimal variations in ionic radii of transition metal ions investigated. The conductometric analysis is based on changes in the electrical conductivity values of solutions as a result of complex formation. These changes depend on the number of ions present, and their mobility’s. Conductivity measurements are employed to trace the different types of chelate species formed between metal ions and STZ. Figure 5 shows the conductometric titration curve for the binary ligand system containing Ti(II), Zr(IV), Sr(II), Al(III), Cr(III), Fe(III), Th(IV), Pb(II), La(III) and Co(II) ions. As can be seen, an initial decrease in conductance and a minimum at (1:1).This may be due to the neutralization of H+ ions resulting from the formation of the (M (STZ)) complex. Furthermore, the conductance
Figure 4. Effect of ionic strength on the stability constants of STZ with metal ions.
Figure 5. Representative conductometric titration curves of 25 mL 0.001 M metal ions with 0.001 M STZ: (a) Al(III); (b) Zr(IV); (c) Co(II); (d) Pb(II) and (e) Cr(III).
increases slightly between (1:1), (1:2) and/or (1:3), probably due to the formation of the binary ligand complex and the release of H+ ions from STZ.
3.4. Species Distribution Diagrams of STZ
Distribution curves of STZ at I = 0.01M NaClO4 shown in Figure 6 observe the pH range (2.20 - 4.80) the major species is α̥ (H2-STZ) and in the pH range (4.80 - 6.00) the major one is α1 (H-STZ-1), but α2 (STZ-2) is major in the pH range (6.00 - 11.40). The species distribution curves can be obtained by plotting the mole fraction of metal species and pH. The curves are depicted in Figure 7. The analysis of these diagrams reveals that at low pH value, most of the metal ions are often present as free ions. This indicated that no complex occur in the acidic medium. On increasing the concentration of the ligand by increasing the pH of the solution during the titration, the mole fraction of the free metal ion tends to decrease, while that of ML species tend to develop at moderately acidic media. However, the value of indicates that there will be an appreciable
Figure 6. Ionic equilibria of STZ in different pH’s range.
Figure 7. Representative ionic equilibria of Al(III)-STZ in different pH’s range.
concentration of ML species in this pH region. Further increasing the pH of the solution, the essential change is the increase in ML2 concentration with decrease in ML. Above this region almost the entire metal ion remains in the form of ML or ML2 species on increasing the pH of the solution. Some fraction species at intersection points and maximum pH, complexes are represented.
3.5. Ternary Systems
The stability constants for the ternary systems were computed from titrations in which the concentrations of metal ions: STZ: Gly were kept in the ratio 1:1:1, listed in Table 2. The experimental data shown in Figure 8 reveal that the formation of the ternary complex M (STZ) (Gly) shifts the buffer region of the ligands to lower pH values, which indicates that the ternary complex is more stable than the binary complex. The horizontal distance between curves e and f
Figure 8. Representative potentiometric titration curve for Al (III)-STZ-Gly system, at 0.1 M NaClO4 and 25˚C ± 0.1˚C: (a) 0.01 M HClO4; (b) a + 0.001 M STZ; (c) b + 0.001 M Al (III); (d) a + 0.001 M Gly; (e) d + 0.001 M Al (III) and (f) a + 0.001 M STZ + 0.001 M Gly + 0.001 M Al (III).
Table 2. Proton ligand formation constants of STZ and stability constant of ternary complexes formed in this study at 0.1 M NaClO4 and 25˚C ± 0.1˚C.
were measured and used for the calculation of (average number of secondary ligand (L) molecule attach edper (M-STZ) binary complex using Equation 4:
(4)
where V1, V2, V3, and V4 are the volumes of NaOH required to reach the same pH values for solutions of (free acid), (free acid + STZ), (free acid + STZ + metal ion) and (free acid + STZ + metal ion + Gly), respectively. The difference can be used for the calculation of (average number of secondary ligand molecules associated with one ion. The free secondary ligand exponent, pLmix was calculated using Equation (5):
(5)
According to the obtained results, the complex equilibria of M-STZ-Gly can be represented by the following scheme:
(6)
(7)
(8)
In order to compare the stabilities of the ternary complex species with those of the parent binary complexes, the ∆logK value (the difference between the stabilities of the binary and the ternary complexes) were determined. The parameter ∆logK is determined by Equation (9):
(9)
It was found that the difference was positive in terms of stability and showed a statistical increase in the value of stability constants of the mixed ligand complex. As shown in Table 2, the values of ternary stability constants are found to decrease in this order: Al(III) > Ti(II) > Pb(II) > Th(IV) > Zr(IV) > Sr(II) > La(III) > Cr(III) > Co(II) > Fe(III)
Formation curves corresponding to the various metal ions-STZ-Gly systems were obtained by plotting vs. pLmix, the results are shown in Figure 9. Values of the formation constant of the STZ ternary complexes (tabulated in Table 2) shows that, the metal ions such as Al(III) and Th(IV) used in M-STZ-Gly ternary complexes are more stable than the (1:1) M-STZ binary complex and
Figure 9. Representative M-STZ-Gly formation curves: (a) Al(III); (b) Pb(II); (c) Zr(IV); (d) Th(IV) and (e) Sr(II).
the (1:1) M-Gly binary complexes. Thus, the (1:1) M-STZ complex has a greater tendency toward combination with Gly molecule to form ternary complexes. But some metal ions viz; Fe(III), Cr(III), La(III) and Co(II) forms less stable ternary complexes with STZ and Gly than the other corresponding binary complexes of them. Therefore, the binary complexes of the primary ligand (STZ) with these metal ions may be at odds with the combination with the Gly molecule to form ternary complexes. On the other hand, some metal ions like, Pb(II), Sr(II), Ti(II) and Zr(IV) have up-normal values. This behavior may be interpreted on the basis of statistical considerations and the nature of species formed in the solution.
4. Conclusion
In the present article, the protonation and complex formation constants of binary and ternary complexes of sulphathiazole end glycine with different metal ions were calculated using potentiometric and conductometric Methods in 25˚C ± 0.1˚C and I = 0.1 M NaClO4 in 25% (v/v) pure ethanol-water medium. The order of stability of the formed binary and ternary complexes was presented. The experimental ∆logK parameters were calculated, showing the effect of the bound primary ligand toward an incoming secondary ligand. ∆logK values are positive; this indicates that the ternary complexes are more stable than the corresponding binary ones. The reported data in this study will make an important contribution to the literature.
Acknowledgements
This work was supported by the Institute of Research and Consulting Studies at Umm Al-Qura University (Project ID: 43603042).
Cite this paper
Al-Rashdi, A.A., Naggar, A.H., Farghaly, O.A., Mauof, H.A. and Ekshiba, A.A. (2018) Potentiometric Determination of Stability Constants of Sulphathiazole and Glycine-Metal Complexes. American Journal of Analytical Chemistry, 9, 99-112. https://doi.org/10.4236/ajac.2018.93009
References
- 1. Domagk, G. (1935) A Contribution to the Chemotherapy of Bacterial Infections. Deutsche Medizinische Wochenschrift, 6, 250-253. https://doi.org/10.1055/s-0028-1129486
- 2. Thiele-Bruhn, S.J. (2003) Pharmaceutical Antibiotic Compounds in Soils—A Review. Journal of Plant Nutrition and Soil Science, 166, 145-167. https://doi.org/10.1002/jpln.200390023
- 3. Zani, F. and Vicini, P. (1998) Antimicrobial Activity of Some 1,2-Benzisothiazoles Having a Benzenesulfonamide Moiety. Archiv der Pharmazie, 331, 219-223. https://doi.org/10.1002/(SICI)1521-4184(199806)331:6<219::AID-ARDP219>3.0.CO;2-U
- 4. Maren, T. (1976) Relations between Structure and Biological Activity of Sulfonamides. Annual Review of Pharmacology and Toxicology, 16, 309-327. https://doi.org/10.1146/annurev.pa.16.040176.001521
- 5. Supuran, C.T., Scozzafava, A., Jurca, B.C. and Iiies, M.A. (1998) Carbonic Anhydrase Inhibitors—Part 49: Synthesis of Substituted Ureido and Thioureido Derivatives of Aromatic/Heterocyclic Sulfonamides with Increased Affinities for Isozyme I. European Journal of Medicinal Chemistry, 33, 83-93. https://doi.org/10.1016/S0223-5234(98)80033-0
- 6. Blasco, F., Perelló, L., Latorre, J., Borrás, J., Garciá-Granda, S. and Inorg, J. (1996) Cobalt(II), Nickel(II), and Copper(II) Complexes of Sulfanilamide Derivatives: Synthesis, Spectroscopic Studies, and Antibacterial Activity. Crystal Structure of [Co(sulfacetamide)2(NCS)2]. Journal of Inorganic Biochemistry, 61, 143-154. https://doi.org/10.1016/0162-0134(95)00053-4
- 7. Topacli, A. and Kesimli, B. (2001) Investigation on Sulfanilamide and Its Interaction with Some Metals and Lincomycin by Infrared Spectroscopy. Spectroscopy Letters, 34, 513-526. https://doi.org/10.1081/SL-100105097
- 8. Karthikeyan, G., Mohanraj, K., Elango, K.P. and Girishkumar, K. (2006) Synthesis and Spectral Characterization of lanthanide Complexes with Sulfamethoxazole and Their Antibacterial Activity. Russian Journal of Coordination Chemistry, 32, 380-385. https://doi.org/10.1134/S1070328406050113
- 9. Golzar, H. (2013) Synthesis and Characterisation of Cobalt Complex of Sulfathiazole with Acetic acid. Journal of Saudi Chemical Society, 17, 253-257. https://doi.org/10.1016/j.jscs.2011.04.002
- 10. Bellú, S., Hure, E., Trapé, M., Trossero, C., Molina, G., Drogo, C., Williams, P.A.M., Atria, A.M., Acevedo, J.C.M., Zacchino, S., Sortino, M., Campagnoli, D. and Rizzotto, M. (2005) Synthesis, Structure and Antifungal Properties of Co(II)-Suifathiazolate Complexes. Polyhedron, 24, 501-509. https://doi.org/10.1016/j.poly.2004.12.017
- 11. Henderson, W., McCaffrey, L.J., Dinger, M.B. and Nicholson, B.K. (1998) Platinum (II) and Palladium (II) Complexes Derived from the Anion of Sulfathiazole [4,2]; Crystal Structure of Cis-[Pt (STZ)2(PPh3)2].3CHCl3. Polyhedron, 17, 3137-3144. https://doi.org/10.1016/S0277-5387(98)00078-3
- 12. Bellú, S., Hure, E., Trapé, M., Rizzotto, M., Sutich, E., Sigrist, M. and Moreno, V. (2003) The Interaction between Mercury(II) and Sulfathiazole. Quimica Nova, 26, 188-192. ttps://doi.org/10.1590/S0100-40422003000200008
- 13. Nunes, B., de Paiva, F., Cuin, A., Lustri, R. and Corbi, P. (2015) Silver Complexes with Sulfathiazole and Sulfamethoxazole: Synthesis, Spectroscopic Characterization, Crystal Structure and Antibacterial Assays. Polyhedron, 85, 437-444. https://doi.org/10.1016/j.poly.2014.09.010
- 14. Daniele, P., Zerbinati, O., Zelano, V. and Ostacoli, G. (1998) Thermodynamic and Spectroscopic Study of Copper(II)-glycyl-L-histidylglycine Complexes in Aqueous Solution. Journal of the Chemical Society, Dalton Transactions, 10, 2711-2715.
- 15. Amrallah, H., Abdalla, A. and El-Haty, Y. (1998) Mixed Ligand Complexes of Benzimidazole and Pyrimidine Hydroxyazo Dyes with Some Transition Metals and Glycine, DL-Alanine or DL-Leucine. Talanta, 46, 491-500. https://doi.org/10.1016/S0039-9140(97)00218-X
- 16. Inci, D. and Aydin, R. (2017) Potentiometric Studies on Complexation of Cu(II) Ion with Methyl/Nitro-Substituted 1,10-Phenanthrolines and Selected Amino Acids. Journal of Solution Chemistry, 46, 124-138. https://doi.org/10.1007/s10953-016-0551-1
- 17. Rossotti, F. and Rossotti, H. (1961) The Determination of Stability Constants and Other Equilibrium Constants in Solution. 4th Edition, McGraw-Hill Book Company Inc., New York.
- 18. Kirschner, S., Wei, Y., Francis, D. and Bergam, J. (1966) Anticancer and Potential Antiviral Activity of Complex Inorganic Compounds. Journal of Medicinal Chemistry, 9, 369-372. https://doi.org/10.1021/jm00321a026
- 19. Mohamed, A., Wadood, A. and Farghaly, O. (2002) Potentiometric and Spectrofluorimetric Studies on Complexation of Tenoxicam with Some Metal Ions. Journal of Pharmaceutical and Biomedical Analysis, 28, 819-826. https://doi.org/10.1016/S0731-7085(01)00691-4
- 20. Abdel Gaber, A., Farghaly, O., Ghandour, M. and El-Said, H. (2000) Potentiometric Studies on Some Cephalosporin Complexes. Monatshefte für Chemie/Chemical Monthly, 131, 1031-1038. https://doi.org/10.1007/s007060070034
- 21. Yousef, W., Alenezi, K., Naggar, A., Hassan, T., Bortata, S. and Farghaly, O. (2017) Potentiometric and Conductometric Studies on Complexes of Folic Acid with Some Metal Ions. International Journal of Electrochemical Science, 12, 1146-1156. https://doi.org/10.20964/2017.02.06
- 22. Scott, W. and Furman, H. (1962) Standard Methods of Chemical Analysis. 6th Edition, Van Nostrand, New York.
- 23. Irving, H. and Williams, R.J.P. (1948) Order of Stability of Metal Complexes. Nature, 162, 746-747. https://doi.org/10.1038/162746a0











