Open Journal of Inorganic Non-metallic Materials
Vol.04 No.02(2014), Article ID:45154,7 pages
10.4236/ojinm.2014.42003
Optical Functions, Band Structure and Effective Masses of Electrons and Holes in InGaTe2
Eldar Gojaev1*, Ulker Abdurahmanova1, Zakir Dzhakhangirli1,2, Shafiga Mehdieva1
1Azerbaijan Technical University, Baku, Azerbaijan
2Institute of Physics, ANAS, Baku, Azerbaijan
Email: *geldar-04@mail.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 December 2013; revised 13 January 2014; accepted 20 January 2014
ABSTRACT
This paper has presented results of calculations of optical functions for e||c and e^c polarizations in 0 - 12 eV energy interval, band structure and effective masses of electrons and holes of ternary compound InGaTe2. Genesis of valence band was investigated by using group-theoretical analyses. The main features of spectra of optical functions, the parameters of transition and their theoretical nature were found out. Identified interband transitions are responsible for the main peaks in the optical functions. Calculated results are in good agreement with the known experimental data.
Keywords:
Optical Functions, Effective Mass, Band Structure, Optical Conductivity, Compound InGaTe2

1. Introduction
It is known that search of new semiconductor materials is usually conducted in the direction of expansion of crystal structure group of already known materials. In particular interpretation of crystal structure of TlSe, it is revealed that this phase differs from extreme specific features. The lattice of TlSe is made of two independent structural units from eight-vertex polyhedron with ionic nature of binding of Tl+-Se and a tetrahedron with covalent binding between Tl3+-Se and therefore, the chemical formula of TlSe should be written as Tl+Tl3+Se2. Thus, by replacement of trivalent atom of thallium corresponding trivalent atoms, in particular, gallium and indium in a lattice of TlSe are received a new class of semiconductor compounds of type. X-ray diffraction researches [1] - [3] showed that part of these compounds has chain structure, and other parts have layered structure. Compounds with chained structure crystallize in a tetragonal syngony, space group 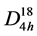 (I4/mcm). On researches of crystal and band structure, optical properties of compounds of TlInSe2 (Te2), TlGaTe2, InGaSe2 (Te2) in domestic and foreign literature there are many data [4] - [10] . However, calculation of band structure with use of modern methods and programs, the system analysis, identification of results of band of InGaTe2 having chained crystal structure weren’t carried out.
(I4/mcm). On researches of crystal and band structure, optical properties of compounds of TlInSe2 (Te2), TlGaTe2, InGaSe2 (Te2) in domestic and foreign literature there are many data [4] - [10] . However, calculation of band structure with use of modern methods and programs, the system analysis, identification of results of band of InGaTe2 having chained crystal structure weren’t carried out.
In this work, results of calculation of optical functions and effective masses of electrons and holes of compound InGaTe2 crystallizing in a tetragonal syngony have been presented. In these calculations the pseudo-po- tential method is used.
Semiconductor compound InGaTe2 crystallizes in a tetragonal lattice with space group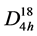 . The unit cell of a crystal contains two formula units. In a crystal lattice monovalent atoms of In are surrounded with eight atoms of Te while trivalent atoms of Ga are in a tetrahedral environment of atoms of Te, and form chains of atoms
. The unit cell of a crystal contains two formula units. In a crystal lattice monovalent atoms of In are surrounded with eight atoms of Te while trivalent atoms of Ga are in a tetrahedral environment of atoms of Te, and form chains of atoms  extended along an optical axis. The growth, the photoemission spectra and properties of single crystals of InGaTe2 are investigated in [11] . So far the band structure and optical characteristics practically are not studied.
extended along an optical axis. The growth, the photoemission spectra and properties of single crystals of InGaTe2 are investigated in [11] . So far the band structure and optical characteristics practically are not studied.
2. Method of Calculation
The band structure and optical functions of InGaTe2 were calculated using pseudopotential method. Calculation of an electronic structure was carried out by DFT, with the help ABINIT software package, using Troiller-Mar- tins pseudopotentials in basis of plane waves. In expansion of wave function plane waves with the maximum kinetic energy of 30 Ry were used. Lattice parameters were defined by total energy minimization and structure parameters were optimized by means of Gelman-Feynman forces.
Minimization process was carried out until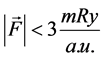 . The optimized lattice parameters and chalcogen parameter: а = 8.3945 Å, с = 6.8352 Å, х = 0.1730 Å.
. The optimized lattice parameters and chalcogen parameter: а = 8.3945 Å, с = 6.8352 Å, х = 0.1730 Å.
Band structure calculation was carried out in symmetric points Г, T, N, P and on the lines connecting these points. The table of irreducible and double irreducible representations of wave vector groups for space group 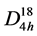 (I4/mcm) were obtained in [12] . Here also are demonstrated condition of compatibility between irreducible representations of simple groups and double-group and Brillouin zone for volume-centered tetragonal lattice.
(I4/mcm) were obtained in [12] . Here also are demonstrated condition of compatibility between irreducible representations of simple groups and double-group and Brillouin zone for volume-centered tetragonal lattice.
In [13] stated band structure of InGaTe2. The lowest subband consisting of four states, about ~6 eV are remote from the others with wide energy gap. Group-Theoretical Analysis shows that these bands located about −10 - −11 eV are obliged by the origin to 5 s-states of Te. The following group of four valence bands located at about −5 eV energy region, comes generally from s-states of atoms of In and Ga. The remained big group consisting of ten bands with 5 eV wide occurs from р-states of atoms of In, Ga and Te. The X-ray photoemission structure of a valence band is given in [13] . It is revealed that the photoemission structure consists of three pronounced areas. Authors attributed peak at −11.5 eV to 5 s-states of Te, peak about −4 eV to Ga-Te bonds, and a complex features about −5 - 0 eV to Ga-Ga and Ga-Te bonds that are accordance with our band structure calculation and the group-theoretical analysis. Energy gap from our calculations turns out 0.56 eV.
Optical functions were calculated by the way described in [14] . For calculation of spectral dependence of imaginary part of complex dielectric permeability we used:
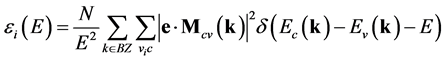 (1)
(1)
Here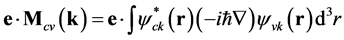 , the integral taken over the unit cell volume and
, the integral taken over the unit cell volume and 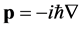 is impulse operator; indexes v and c number indicates valence and conduction bands, respectively, е-vector of polarization.
is impulse operator; indexes v and c number indicates valence and conduction bands, respectively, е-vector of polarization.
In summation over Brillouin zone in (1) elementary cell of the reciprocal lattice is divided into 64 equal parts on volume, and in them k points were chosen randomly. Calculations were carried out at 3000 k points for smooth histogram. N is defined from a normalization condition
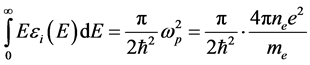
where 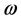 -plasma frequency of electrons,
-plasma frequency of electrons, 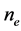 -the average density of electrons in a crystal.
-the average density of electrons in a crystal.
The histogram was constructed with 0.2 eV energy step and covered all interband transitions v ® c up to 12 eV. Further εi(E) dependence was extrapolated by known formula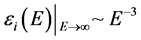 . Transitions from the lowermost zones belonging to Te-5 s, apparently, get to the studied spectral area. These states are located far from others and according to our investigations, the broadening of the spectral region, and thus involvement greater energy transitions from the high-lying regions in the conduction state does not lead to contribution in the dielectric constant, so not differs considerably from extrapolation.
. Transitions from the lowermost zones belonging to Te-5 s, apparently, get to the studied spectral area. These states are located far from others and according to our investigations, the broadening of the spectral region, and thus involvement greater energy transitions from the high-lying regions in the conduction state does not lead to contribution in the dielectric constant, so not differs considerably from extrapolation.
The real part of dielectric permeability is defined from cramers-kronig relations in Equation (2)
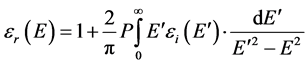 (2)
(2)
here the symbol P is principal value of integral.
3. Results and Discussion
Results of calculations of spectral functions εr(E) and εi(E) for e||c and e^c polarizations are given in Figure 1. As can be seen from Figure 1(a) in the energy range of 1.6 - 3.15 eV in e||c polarization functions increases rapidly to a maximum. According to these figures the maximum of the main peak in the spectrum of εr(E) in the polarization e||c (Figure 1) is located at an energy of 3.15 eV, and for e^c (Figure 1) at 2.61 eV, and the main maximum in the εi(E) in both polarizations, which we associate with the transitions from the top of the valence band to the bottom of the conduction band are at 3.15 eV. In the spectrum of εi(E) and in the e^c polarization there are three peaks with the energies of 4.02, 5.9, 6.2 and 7.47 eV.
In e||c the polarization additional peaks located at energies of 3.9, 6.2 and 7.8 eV, but they, especially the last, are weak. The maximum value in e||c polarization is 15.1, and in e^c polarization is 12.8, such difference in value for different polarizations is characteristic for chained crystals with strong anisotropy.
Limiting value of εr(E = 0) is equal to 7.88 in e||c polarization and 7.21 in e^c polarization.
The main part of refraction index was determined by Equation (3):
 , (3)
, (3)
Figure 2(a) shows the energy dependence of the main index of refraction. In e||c energy dependence of 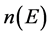 begins with the value
begins with the value 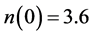 and reaches maximum at energy 3.15 eV (3.62) and a pronounced minimum at the energy 2,61 eV (2.87) and one more minimum at the energy 8.35 eV (0.17) and further growth of
and reaches maximum at energy 3.15 eV (3.62) and a pronounced minimum at the energy 2,61 eV (2.87) and one more minimum at the energy 8.35 eV (0.17) and further growth of 
The imaginary part of the refractive index is defined as (4),

In Figure 2 spectral dependence of imaginary part of the refractive index of InGaTe2 is presented.

Figure 1. Spectral dependence of imaginary (a) and real (b) parts of dielectric constant of InGaTe2 for e^c and e||c polarizations.


Figure 2. Energy dependence real (a) and imaginary (b) parts of indicators of refraction of InGaTe2 in e||c and e^c polarizations.
For polarization e||c dependence begins with 2.1 eV, then there is an increase in imaginary part of coefficient refraction reaching a maximum at energy of 3.9 eV (2.53), then monotonous reduction and a minimum at energy of 8.3 eV (0.39) and increase to 9.6 eV (0.52) other areas of dependence. In e^c polarization dependence begins with very small energy of equal 0.12 eV, at 3.15 eV (1.93) and 4.02 eV (1.99) two maxima are observed, at energy of 3.65 eV (1.7) and between maxima there is a minimum further dependence monotonously the pronounced maximum decreases and observed at 6.23 eV (4.72) a minimum at 6.88 eV (1.11), a maximum at 7.47 eV (1.19) and further reduction with increase in energy.
For e e||c polarization 




The reflection coefficient at normal incidence of light is defined by a Formula (5):

Spectral dependence of Reflectivity of InGaTe2 is given in Figure 3 (and) for e||c and e^c of polarization. The maximum of reflection in polarization parallel to optical axis of a crystal is at energy of »3.9 eV (0.46), and two minima located at energy of »2.61 eV (0.30), »5.93 eV (0.29). In polarization perpendicular to optical axis the main maxima are at »3.15 energy eV (0.4), »6.23 eV (0.66), and minima at »5.98 eV (0.29), »6.89 energy eV (0.22).
Figure 3(a) shows the spectral dependence of the reflection coefficient of InGaTe2 for e||c and e^c polarizations. The maximum of the reflection coefficient in the polarization parallel to the optic axis is at an energy »3.9 eV (0.46), and two minima at energies »2.61 eV (0.30), »5.93 eV (0.29). In polarization perpendicular to the optical axis of the crystal main peaks occur at energies »3.15 eV (0.4), »6.23 eV (0.66), and minima at the energies »5.98 eV (0.29), »6.89 eV (0.22). The Characteristic Electron Energy Loss function was shown by (6)

The spectral characteristic of imaginary part of an inverse value of complex dielectric permeability


Figure 3. Spectral dependences of coefficient of reflectivity and imaginary part of an inverse value of complex dielectric permeability InGaTe2 compound in e^c and e||c polarizations.
is presented in Figure 3. As seen from figure in e||c polarization are observed two maxima at energy 7.096 eV (0.45) and a minimum at 8.3 eV (3.93).
In polarization e^c maxima appear at energy of 6.89 eV (0.41) and 8.2 eV (0.71), and minima at energy of 1.66 eV (0.01) 6.22 eV (0.02).
Real and imaginary parts of optical conductivity were defined by Formula (7):

Dependence 
From here two bright minima are visible at energy of 2.61 eV (13.27), 4.57 eV (−8.6) and pronounced maxima at energy of 3.15 eV (21.18), (e||c).And for polarization e^c, the weak minimum here is observed at 3.65 eV (9.79), the bright maximum at 2.66 eV (21.15) and for both polarization occurs further weak reduction
Components of inverse effective mass tensor were determined by the formula


Figure 4. Spectral dependences real and imaginary part optical conductivity of InGaTe2 compound in e^c and e||c polarizations.
m0-electron rest mass: 

operator 



V-volume of elementary cell, En(k0) and 

Calculation of band structure shows that maximum of valence and minimum of conduction bands are located at high symmetry point T of k0 = 0.5b1 − 0.5b2 + 0.5b3 (b1, b2, b3). Here b1, b2, b3 are translation vectors of reciprocal lattice.
In our calculations components of tensor of inverse effective mass of electron were calculated with an accuracy to 0.01 m0.
Components of tensor of inverse effective mass of holes is given by
As can be seen tensors of inverse effective mass of both electrons and holes have diagonal form and therefore isoenergetic surfaces are described by rotational ellipsoids that is corresponds to symmetry of crystal.
4. Conclusion
So, in this report the spectra of optical fundamental functions of the semiconductor InGaTe2 have been calculated for two polarizations e||c and e^c in 0 - 12 eV energy range for the first time. Parameters have been defined, effective masses of electrons and holes of compound InGaTe2 were calculated on the basis of the band structure. The results obtained allow a detailed analysis of the optical properties and electronic structure of InGaTe2.
References
- Hahn, H. and Weltman, B. (1967) Üder ternare chalkogenide des Thalliums mit Gallium und Indium. Naturwissenschaften, 54, 42. http://dx.doi.org/10.1007/BF00680166
- Müller, D., Eulenberger, G. and Hahn, H. (1973) Über ternare Thalliumchalkogenide mit thalliumsselennidstructur. Zeitschrift für anorganische und allgemeine Chemie, 398, 207-220. http://dx.doi.org/10.1002/zaac.19733980215
- Mooser, E. and Pearson, W.B. (1956) The Chemical Bond in Semiconductors. Journal of Electronic and Control, 1, 629-645.
- Godzhayev, E.M., Allakhyarov, E.A. and Sadykhova, H.O. (1994) Tensometric Properties Single Crystals TlInTe2. Russian Academy of Sciences. Inorganic Materials, 30, 859.
- Orudzhev, G., Mamedov, N., Uchiki, H., Yamamoto, N., Iida, S., Toyota, H., Gojaev, E. and Hashimzade, F. (2003) Band Structure and Optical Functions of Ternary Chain TlInSe2. Journal of Physics and Chemistry of Solids, 64, 1703- 1706. http://dx.doi.org/10.1016/S0022-3697(03)00073-8
- Godzhayev, E.M., Orudzhev, G.S., Kerimova, R.A. and Allakhyarov, E.A. (2006) Band Structure and Optical Properties of Chained Compound TlInTe2. Physics of a Firm Body, 48, 40-43.
- Godzhayev, E.M., Pashayev, A.M., Movsumov, A.A., Halilova, H.S. and Agayeva, S.H. (2010) Akustofotovoltaic Effects in TlIn0.98Cd0.02Se2 Monocrystals. Inorganic Materials, 46, 20-23.
- Godzhayev, E.M., Gyulmamedov, K.D., Halilova, H.S. and Guliyeva, S.O. (2011) Effect of Switching on Thin Films of TlInSe2. Electronic Processing of Materials, 47, 18-22.
- Godzhayev, E.M., Orudzhev, G.S. and Kafarova, D.M. (2004) Band Structure and Dielectric Permeability of the Compound InGaTe2. Physics of the Solid State, 46, 833-835. http://dx.doi.org/10.1134/1.1744956
- Godzhayev, E.M., Jahangirli, Z.A., Alieva, P., Khalilova, K. and Musaev, T. (2013) The Growth of Single Crystals of InGaSe2 Compounds, Their X-Ray-Phase Analysis, Electronic Structure and Optical Functions. Journal of Inorganic Non-Metallic Materials, 3, 1-5. http://dx.doi.org/10.4236/ojinm.2013.31001
- Mobarak, M., Berger, H., Lorusso, G.F., Capozzi, V., Perna, G., Ibrahinl, M.M. and Margaritondo, G. (1998) The Growth and Properties of Single Crystals of InGaTe2, Ternary Chalcogenide Semiconductor. Journal of Physics D Applied Physics, 3, 1433-1437.
- Hashimzade, F.M. (1960) The Symmetries of Energy Bands of TlSe Type Crystals. Physics of the Solid State, 2, 3040-3044.
- Godzhayev, E.M., Dzhakhangirli, Z.A., Allakhyarov, E.A., Kafarova, D.M. and Ibragimova, A.R. (2011) Cultivation, Phase Analysis and Band Structure of a Monocrystal of InGaTe2. Inorganic Materials, 47, 1162-1165.
- Ukhanov, Y.I. (1977) Optical Properties of Semiconductors. Nauka Publishers, Moscow.
NOTES
*Corresponding author.









