Open Journal of Composite Materials
Vol.06 No.02(2016), Article ID:65328,17 pages
10.4236/ojcm.2016.62005
Out of Plane Thermal Conductivity of Carbon Fiber Reinforced Composite Filled with Diamond Powder
M. Srinivasan1*, P. Maettig1, K. W. Glitza1, B. Sanny1, A. Schumacher2, M. Duhovic3, J. Schuster4
1Department of Experimental Physics, University of Wuppertal, Wuppertal, Germany
2Department of Mechanical Engineering, University of Wuppertal, Wuppertal, Germany
3Institute for Composite Materials, Kaiserslautern, Germany
4University of Applied Sciences Kaiserslautern, Pirmasens, Germany

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 January 2016; accepted 3 April 2016; published 6 April 2016
ABSTRACT
Highly conductive fillers have a strong influence on improving the poor out of plane thermal conductivity of carbon fiber reinforced composites. The objective of this study has been to investigate the role of the diamond powder (DP) in enhancing the out-of-plane thermal conductivity of the woven composites. Samples of the standard modulus T300 carbon fiber composite with 44% and 55% fiber volume fraction and the high modulus YS90A carbon fiber composite with 50% volume fraction were fabricated with their matrices comprising of neat epoxy and different loading of diamond powder within epoxy resin. Steady state thermal conductivity measurements were carried out and it was found from the measurements that the out of plane thermal conductivity of the standard modulus composite increased by a factor of 2.3 with 14% volume fraction of diamond powder in the composite while the out of plane thermal conductivity of the high modulus composite increased by a factor of 2.8 with 12% volume fraction of diamond powder in the composite. Finite Element Modeling (FEM) with the incorporation of microstructural characteristics is presented and good consistency between the measurements and FEM results were observed.
Keywords:
Carbon Fibers, Thermal Conductivity, Finite Element Analysis (FEA), Micro-Mechanics, Thermal Measurements

1. Introduction
Polymer-matrix composites with continuous carbon fiber are important for many high technology industrial or research applications. Examples are lightweight structural materials in aerospace industry for aircraft radiators, directed energy mirror structures, satellites, missiles [1] . The research and development reported in this paper have been conducted in the framework of the experiments for particle physics, such as at the Large Hadron Collider (LHC) [2] at the European Organization for Nuclear Research (CERN). Here light weight but very stable support structures for high precision sensors are required with the additional constraint to remove the heat produced from the read-out electronics and the sensors themselves. Carbon fiber reinforced composites are used in this case to provide mechanical support and protection from thermal runaway of the detector. This study has been intended to investigate the improvements of thermal properties of the composite, with the intention of improving the thermal behavior of the support structure (Figure 1) of pixel detector of the ATLAS experiment [3] at the LHC.
To define the environment and challenges of this application can be exemplified with the insertable B-Layer (IBL) [4] , which has recently been installed into ATLAS. Its local support structure of the subdetector is shown in the Figure 1(a) and Figure 1(b). It is about 800 mm long and designed to hold the sensors and electronics in positions with high accuracy of a few, minimizing the deformation induced by the cooling and at same time keeping the temperature of the sensors at a constant temperature of about −20˚C in order to minimize radiation damage and prevent thermal runaway, while the electronics on the pixel sensors produce a relevant amount of heat. This power is removed by a Titanium cooling pipe runs through the support structure to provide an evaporative CO2 boiling system. The thermal contact between the electronics and the cooling pipe is made through a highly thermally conductive light carbon foam. Titanium has a thermal conductivity higher than the carbon fiber but the titanium induces the potential problem of a coefficient of thermal expansion (CTE) mismatch with the carbon foam. Furthermore it has a small radiation length, and therefore distorts the tracks of charged particles and reduces the measurement precision. With the focus on future upgrade of pixel detector, new support structures have to be developed with a reduced material budget, but with an enhanced thermal, thermomechanical behavior so that the support structure can operate with much improved performance under the significantly harsher conditions after the LHC upgrade high. Instead of a metallic cooling pipe one made of carbon fiber would avoid some of the problems mentioned above. On the other hand, normally these carbon materials have a rather low out of plane thermal conductivity (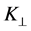 ). In this paper it is shown that this can be significantly improved by using diamond powder as filler of the matrix of carbon fibers.
). In this paper it is shown that this can be significantly improved by using diamond powder as filler of the matrix of carbon fibers.
Thermal Properties of Composites
The favourable specific properties of carbon fiber reinforced polymer composites are based on the low density of the matrix resins used and the high strength of the embedded fibers [5] [6] . Woven fabric based composite materials are an attractive option for a range of engineering applications. Although the mechanical properties are not as good as those of their non-woven counterparts, they still offer reasonable specific stiffness and strength with particularly good impact and energy absorption characteristics [6] [7] . PAN (Polyacrylonitrile) and Pitch based carbon fibers are typical reinforcing materials in polymer matrix composites with thermal conductivity in

Figure 1. (a) Local support structure of subdetector (IBL) within ATLAS experiment at CERN; (b) different materials within the support structure [4] .
the range of 15 - 1100 Wm−1∙K−1 in the fiber direction [6] [8] . The pitch based carbon fibers have a large crystal size, excellent electrical and thermal conductivity with high tensile modulus but low elongation. The PAN based carbon fibers have very small crystal size, giving flexibility, very high tensile strength, high elongation but lower thermal conductivity [6] [9] . However, in the through-thickness direction, the thermal conductivity of carbon fiber reinforced composite is no more than 1 Wm−1∙K−1 due to the laminate structure [6] [10] . The high in-plane thermal conductivity promotes heat spreading but low out of plane thermal conductivity hinders heat removal. Both in-plane heat spreading and out of plane heat removal are important for effective heat dissipation [6] [11] . Most polymer resins are known to be thermal insulators. One of the alternative approach for achieving a significant increase in the out of plane thermal conductivity is to manufacture composites based on 3D woven fiber architectures where the through-thickness fibers have high thermal conductivities and the experimental results showed that with a 3D z-fiber volume content of about 6%, the maximum possible out of plane thermal conductivity could be increased by a factor of eight over that of a traditional uniaxial or biaxial laminate composite [12] . Other common approaches for improving the thermal conductivity of a polymeric material, polymer matrices are usually filled with the thermally conductive fillers and some of them are listed in the Table 1 [13] .
Jeon et al. reported that the incorporation of functionalised graphite flakes into epoxy resin yielded a thermal conductivity of 1.53 Wm−1∙K−1 at 10 wt% and an increase in the modulus of 1.03 GPa at 1 wt% than that of the neat epoxy. The loss modulus to the storage modulus ratio ( of the functionalised graphite flakes/epoxy nanocomposite were much lower than that of pure epoxy [14] . This has been attributed to the interaction between the carboxylic group of pyrenebutyric acid functionalized on the surface of the graphite flakes and the epoxy matrix, which enhances interfacial adhesion and restricts the motion of the epoxy segmental chains [14] [15] . Fusao et al. [16] prepared a polymer composite by impregnating the epoxy resin with a network like a- alumina pellet containing 54% volume fraction of a-alumina particles and achieved a thermal conductivity of 4.2 Wm−1∙K−1. Carbon based fillers like single-walled carbon nanotubes (SWNT), multi-walled carbon nano- tubes (MWNT), vapor-grown carbon nanofibers (VCNFs) are being used as fillers for developing thermally conductive resins [17] - [19] and recently Yang et al. observed no detectable change in the thermal conductivity of vapour grown carbon nanofiber (VGCNF) liquid crystal polymer composites with VGCNF content of as high as 15 weight% (wt%), which was attributed to the nonuniform dispersion of nanofibers and the lack of a percolated network between them [20] .
of the functionalised graphite flakes/epoxy nanocomposite were much lower than that of pure epoxy [14] . This has been attributed to the interaction between the carboxylic group of pyrenebutyric acid functionalized on the surface of the graphite flakes and the epoxy matrix, which enhances interfacial adhesion and restricts the motion of the epoxy segmental chains [14] [15] . Fusao et al. [16] prepared a polymer composite by impregnating the epoxy resin with a network like a- alumina pellet containing 54% volume fraction of a-alumina particles and achieved a thermal conductivity of 4.2 Wm−1∙K−1. Carbon based fillers like single-walled carbon nanotubes (SWNT), multi-walled carbon nano- tubes (MWNT), vapor-grown carbon nanofibers (VCNFs) are being used as fillers for developing thermally conductive resins [17] - [19] and recently Yang et al. observed no detectable change in the thermal conductivity of vapour grown carbon nanofiber (VGCNF) liquid crystal polymer composites with VGCNF content of as high as 15 weight% (wt%), which was attributed to the nonuniform dispersion of nanofibers and the lack of a percolated network between them [20] .
Patton et al. observed a 300% increase in the thermal conductivity of vapour grown carbon fiber (VGCF) polymer composites with 39 vol% VGCF, however, the magnitude of the thermal conductivity remained relatively low (0.8 Wm−1∙K−1) as compared to the intrinsic thermal conductivity of the filler and the low magnitude of composite thermal conductivity was attributed to the low efficiency in transfer of thermal energy between nanofibers [21] . Xing et al. reported an increase in thermal conductivity of the polymer composite up to 2.83 with high volume fraction (57.5%) of well-dispersed multi-walled carbon nanotubes and copper nanowires in the epoxy matrix [22] . Wu et al. studied that a vertically aligned MWCNT array embedded in a composite can provide direct channels for transmitting heat and more effectively increase the thermal conductivity of the composite [23] . One of the important concern with the CNTs are towards the uniform dispersion of the nanotube phase within the polymeric matrix and improved nanotube/matrix wetting and adhesion are critical issues in the
Table 1. Thermal conductivity of conventional thermal conductive fillers [13] .
processing of nanocomposites [24] . Another interesting filler material is graphene which is a single layer structure of two-dimensional new carbon material [25] and it has attracted tremendous interest particularly from engineers and scientists due to its unique physical and chemical properties like strong mechanical robustness [26] , excellent thermal conductivities (more than 5000 at room temperature) [27] and large specific surface area (3100 for activation of graphene) [28] .
As graphene is in the early stage of development, there are a few issues related to the production methods as there are no good general synthesis methods that could produce graphene quickly and precisely. Some research has proven that graphene is susceptible to oxidative environments and could exhibit toxic qualities [29] . In comparison, the diamond powder (DP) being a carbon-based filler has a higher thermal conductivity (1000 - 2000 Wm−1∙K−1), excellent corrosion resistance, and a lower thermal expansion coefficient than metal [13] based fillers. Since the diamond's are isotropic, there would not be any necessity for special manufacturing techniques for aligning the DP. It has been previously reported [30] that the mechanical properties of epoxy-diamond composite increased with lower content of diamond powder but with the higher content the mechanical properties decreased due to agglomeration. An understanding of relative behavior of the filler in the composite is valuable for developing methods to predict out of plane thermal conductivity. The objectives of this paper were:
1. To investigate the effect of lower and higher contents of microscale diamond powder (DP) by dispersing it on the dry fabric and also by matrix modification technique towards the out of plane thermal conductivity of PAN (T300 Twill woven fabric) and Pitch based(YS90A Plain woven fabric) composites.
2. To investigate the thermal contact along with the formation of conductive paths in the composite.
2. Experimental Methods
2.1. Materials
PAN based T300 carbon fiber fabric woven in 2/2 Twill was supplied by Cytec Thornel, Inc and Pitch based GRANOC YS90A carbon fiber fabric woven in plain weave was supplied by Nippon Graphite fiber Corporation. Both the fabrics had the fiber diameter of 7. The fabric data and fiber material properties are given in the Table 2. The epoxy and hardener used in the fabrication are commercially available LARIT RIM 135 and LARIT RIM 134. The resin to hardener mixing ratio was 2:1, the pot life was 30 - 45 minutes and the set time was 5 - 6 hours. Diamond Powder with diameter from 0.5 μm to 1 μm, thermal conductivity of 1000 Wm−1∙K−1 and density of 3.5 g∙cm−3 was supplied by AB Industrial Diamonds, Germany. Both T300 and YS90A On-axis (0˚ - 90˚) fabrics had same number of yarns in the weft and warp directions.
2.2. Fabrication of the Samples
2.2.1. Dispersion of Diamond Powder on Dry Fabric
Fabrication of woven fabric composite plates was performed at the Institute for Composite Materials (IVW), Kaiserslautern. The vacuum assisted resin infusion technique was used to fabricate the composite plate. Five layers of 2/2 twill fabric with an areal weight as specified in the Table 2 were used for fabrication of specimens and this related to fiber volume fraction of 55%. The average dimensions of the composite specimens were 70 mm long, 70 mm wide and 2 mm thick. In this technique the diamond powder filler was deposited on the woven carbon fiber fabric prior to impregnation (Figures 2(a)-(c)). The fabrics were weighed after deposition of the diamond powder to know the weight fraction of the diamond powder in the composite. Epoxy resin and hardener were mixed to ratio of 2:1 and the resin mixture was degassed for 20 minutes to remove air bubbles. Vacuum assisted resin infusion was performed (Figure 2(d)) and the composite was cured in an autoclave at a static pressure of 24 bar close to 9 hours (Figure 2(e)). One Sample without diamond powder and one sample with 14% volume fraction of diamond powder in the composite were prepared.
Table 2. Fabric data and fiber material properties.
Figure 2. Deposition of diamond powder on woven carbon fiber fabric (a)-(c); vacuum assisted resin infusion (d); curing in an autoclave (e).
2.2.2. Matrix Modification Technique
Five different types of T300 composite plates were produced with this technique. Four layers of 2/2 twill fabric with an areal weight as specified in the Table 2 were used for fabrication of specimens and this related to a fiber volume fraction of 44%. The first type of the sample was prepared without the diamond powder and the resin mixture was infused by vacuum into carbon fabric during the impregnation process. The remaining four samples were prepared by incorporating diamond powder of different fractions (Table 3) into the epoxy. A vacuum assisted hand layup technique was applied and the samples were cured in an autoclave. In the same way, YS90A samples were also produced where twenty six layers of plain weave fabric (Table 2) with a total fiber areal weight of 3250 g∙cm−2 were used for fabrication of the samples. The average dimensions of the composite specimens were 200 mm long, 250 mm wide and 3 mm thick. One sample without and two other samples with the diamond powder of different fractions as listed in the Table 3 were prepared.
2.3. Thermal Conductivity Measurements
Steady state out of plane thermal conductivity measurements were performed with a measuring cell built in- house at the Institute of Polymer Technology at University of Applied Sciences, Kaiserslautern according to ASTM E1225-04 allowing measurements of circular samples with a diameter of 50 mm at thicknesses (thicknesssample) from 2 to 50 mm [12] [33] [34] . Water-jet cutting was used to prepare spherical specimens of 50 mm diameter, 2 mm thickness for T300 fiber specimens and 3 mm thickness for YS90A fiber specimens (Figure 3(1-6)).
The measuring cylinder shown in the Figure 4 consisted of four individual components namely the outer cylinder, insulating cylinder, meter bar and a cooling plate with a sample holder connected to the bottom of the measuring cylinder. The outer cylinder was connected to a voltage device through which output A of the outer cylinder was controlled, the meter bar was controlled by output B of the voltage device. Four thermistors were used for the temperature measurement at the meter bar and the heating was provided through a cartridge heater in the top meter bar. The height of the two bars Dz including the sample are about 250 mm. Three thermistors in the top meter bar were used to measure the temperatures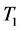 ,
, 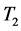 and
and 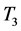 and the temperature
and the temperature 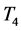 was measured by the thermistor in the bottom meter bar which contacted a cool plate to provide a heat sink with a constant temperature of 20˚C beneath the bottom plate. The top meter bar was made of stainless steel (with a thermal conductivity of
was measured by the thermistor in the bottom meter bar which contacted a cool plate to provide a heat sink with a constant temperature of 20˚C beneath the bottom plate. The top meter bar was made of stainless steel (with a thermal conductivity of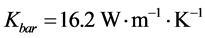 ) and it was insulated with foam and additionally shielded by a guard heater (Figure 4) to prevent the radial heat loss. Conductivity paste (OMEGATHERM201 with a thermal
) and it was insulated with foam and additionally shielded by a guard heater (Figure 4) to prevent the radial heat loss. Conductivity paste (OMEGATHERM201 with a thermal
Figure 3. Composite samples of 50 mm diameter after water-jet cutting: YS90A composite samples without diamond powder (1), with diamond powder volume fraction of 6% (2) and 12% (3) in the composite; T300 composite(fiber volume fraction of 44) samples without diamond powder (4), with diamond powder volume fraction of 0.8% (5) and 3% (6) in the composite.
Figure 4. Measurement setup with the sample.
Table 3. Details of diamond powder contents in the samples.
conductivity of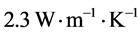 ) and a weight of 1.5 g was weighed twice and was applied on each side of the sample in order to facilitate coupling and to reduce interfacial thermal resistance between meter bars and samples. All the thermistor informations were evaluated by a LabView based program.
) and a weight of 1.5 g was weighed twice and was applied on each side of the sample in order to facilitate coupling and to reduce interfacial thermal resistance between meter bars and samples. All the thermistor informations were evaluated by a LabView based program.
Calibration measurements were performed on isotropic specimens to determine the accuracy of the measuring cell [12] . The materials (like steel, stainless steel, aluminum, polyamide) with known thermal conductivities were measured and the matches were almost perfect with the [12] and the uncertainties were less than ±3. The thermal resistance 
out of plane thermal conductivity of the composite (




and 32˚ respectively. The Test was repeated at least four times in order to obtain the mean value of out of plane thermal conductivity of the composite which are reported in the results and the typical percentage uncertainty (based on the standard deviation) of the measurement data for the standard modulus (T300) and the high modulus (YS90A) composite specimen was 0.71% and 1.06%.

3. Micromechanical Modeling
Generally, periodic models [35] [36] are employed for simplicity, assuming that the material has a deterministic and ordered distribution of fibers. Fiber reinforced composites are far from being periodic materials because the fibers are randomly distributed through the matrix [37] . GeoDict is a software (developed by Math2Market®) for composites uses an integrated approach through mCT scan data allowing the analysis of a broad range of the composite’s material properties as well as thermal conductivity analysis and parameters including damage and failure [38] . Digimat is another software used in multi-scale analyses to predict the nonlinear micromechanical behavior of plastics, composite materials and structures [39] .
In order to have a detailed understanding of out of plane thermal conductivity of the on-axis woven T300 and YS90A fabric composites, micromechanical finite element models were developed in AbaqusTM. An algorithm based on modified random sequential adsorption method was developed to generate the two dimensional unit cell models of random distribution of fibers within the representative volume element(RVE) and diamond powder fillers were randomly distributed within the matrix.
3.1. Algorithm Development-Unit Cell Generation
An algorithm [6] was developed (in Matlab) to generate random distributions of fibers in the unit cell which would be statistically equivalent to the actual carbon fiber reinforced composite microstructure. fibers were generated with the radius r = 3.5 mm in the Representative Volume Element (RVE).
1. The side length of the RVE was kept as L, the radius of fiber as r. The object was considered as a quadrate area, the size of the RVE was represented as d which related to side length of RVE L to the radius of fiber r
using the relationship d = L/r. A random point for the first fiber was created having coordinates 
2. The second point 




[37] . The distance between the center coordinates 


3. If the fiber surface touches the surface of RVE or if they are very close, it may not be possible to mesh or the generated FEM mesh might be distorted. To avoid these situations, the fibers are kept at a minimum distance from the surface of the RVE

4. Steps 2 and 3 were repeated to generate new fibers surrounding the first fiber (Figure 5(c)). Throughout the procedure, checks were performed to ensure the distance between the fiber centers and also the distance from the surface of RVE to make sure the fibers lie within the window.
5. The algorithm was made to move to the second fiber and steps 2, 3 and 4 were repeated.The entire process was repeated to all the fibers thereafter until the desired fiber volume fraction was reached or until the sample area was filled. The fibers were generated through AbaqusTM python scripting.
6. A separate script was developed for generating the number of fillers (with a radius rf = 0.5 mm) and their coordinates based on their specified volume fraction within the RVE. A minimum center distance between the fiber and the diamond filler were specified as shown in the Equation (5) in order to maintain a random fiber-filler distance and another condition was specified to maintain the filler-filler distance which are shown in the Equation (6).


The fillers were generated in the RVE through the python script after knowing their coordinates. The Figure 6 represents the development of RVE based on an algorithm by which YS90A carbon fibers were randomly generated with 50% of fiber volume fraction and 12% volume fraction of Diamond Powder in the RVE.

Figure 5. (a) Assigning a random point for the center of first fiber; (b) assigning second fiber based on nearest neighbor; (c) assigning subsequent fibers [6] .
Figure 6. RVE with randomly generated YS90A fiber of 50% volume fraction and 12% volume fraction of Diamond Powder in the composite.
3.2. Finite Element Modeling
A steady state heat transfer thermal analysis was carried out. Three different sets of FEM were performed;
1. A RVE with randomly generated T300 fibers (44% and 55% volume fractions) and YS90A fibers (50% volume fraction) incorporated with randomly distributed diamond powder within the epoxy matrix and the volume fractions of the diamond powder were maintained at 0.8%, 1.6%, 3%, 8% and 0.7%, 1.4%, 2.7%, 6%, 11%, 14%, 16% and 1.6%, 5%, 6%, 8%, 10%, 12% (Figure 6) of the composite.
The models were meshed with three node linear heat transfer triangular elements DC2D3 (Figure 7(a)). Two temperature conditions were set represented as 

constant temperatures, the heat flux (Q) was calculated by integrating the entire 

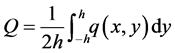
Out of plane thermal conductivity (



4. Results and Discussion
4.1. T300 Composite, 44% Fiber Volume Fraction
The experimental results of the T300 woven composite with a fiber volume fraction of 44% (Figure 8, Table 4) indicated that the effect of diamond powder upto 3% volume fraction was not significant and the out of plane
thermal conductivity of the composite increased from 


Figure 7. AbaqusTM heat transfer triangular element (a) [41] , FEM boundary condition for the model setup (b).
Table 4. Out of plane thermal conductivity (
Figure 8. FEM and experimental results comparison of T300-diamond powder epoxy filled composite with 44% fiber volume fraction.
epoxy was higher than the fiber and diamond powder in the samples and epoxy being an insulator inhibited the fiber-diamond powder filler interaction and filler-filler interaction. FEM results T300 composite with fiber volume fraction of 44% shown in the Figure 8 and Table 4 also predicted the lack of improvement in thermal conductivity at lower diamond powder content. The distance between the inter-filler (diamond powder-diamond powder) and filler-fiber distance were larger at lower diamond powder content and the isolated diamond powder particles did not show any significant effects towards a thermal conductivity improvement and it also resulted in a lack of formation of conductive paths. At 8% diamond powder volume fraction (Figure 8, Table 4), experi- mental and FEM results predicted a linear increase in out of plane thermal conductivity. With higher epoxy content and even when the diamond powder content was increased, the increase in thermal conductivity was again not significant.
4.2. T300 Composite, 55% Fiber Volume Fraction
FEM results with a fiber volume fraction of 55% as shown in the Figure 9, Table 5 also explains the physical phenomenon of a lack of conductive path formation upto 1.4% volume fraction of diamond powder in the composite. From 3% to 11% volume fraction of diamond powder, there was an effect of a rapid increase in the out of plane thermal conductivity. The micromechanical modeling was carried out based on a two step homogenization process (for the matrix and for the composite) by which, an increase in the volume of diamond powder reduced the inter-diamond filler distance, which enhanced the polymer thermal conductive path and with increase in filler content the fiber-diamond filler distance also reduced which increased the network of conductive path for the composite. When the diamond powder volume content increased, interaction between fiber and diamond powder accelerated which led to formation of additional conductive paths and the number of contact points between the diamond powder filler and fibers in the microstructure increased due to a homogeneous distribution of diamond powder in the composite leading to a rapid increase in the out of plane thermal conductivity.
SEM image shown in the Figure 10(a) represents the behavior of fiber-filler (marked in red in the Figure 10(a)) and filler-filler interaction at 15% volume fraction of diamond powder which influence the formation of thermal interface for T300 composite. Figure 10(b) shows the dispersion of the diamond powder in the epoxy matrix. The behavior predicted by the FEM result after 11% volume fraction content of diamond powder showed a saturation, where with the further increase in the filler content, the influence was not significant (Figure 9, Table 5) where the thermal conductivity of the fibers determine the overall thermal conductivity of the composite and the effective conductive path formation by the diamond powder becomes nullified even by increasing the content of the diamond powder. This saturation point has been reported by Shan-Tung Tu et al. as a physical property ratio which happens with the increase of volume fraction of the fillers and beyond this saturated ratio, the physical properties of the composites cannot be further improved by enhancing the corresponding property of the matrix material [42] .
Figure 9. FEM and Experimental results comparison of T300-diamond powder epoxy filled composite with 55% fiber volume fraction.

Figure 10. SEM images showing fiber-diamond filler matrix forming thermal interface (marked in red) in the T300 composite(55% fiber volume fraction) with 15% volume fraction of the diamond powder (a); dispersion of the diamond powder in the epoxy matrix (b).
Table 5. FEM and the experimental results for the out of plane thermal conductivity of T300 composite (fiber volume fraction of 55%).
4.3. YS90A Composite
High modulus YS90A fiber being highly conductive showed an interesting behavior where the significance of the diamond powder towards the out of plane thermal conductivity at the volume content below 5% in the composite was again minimal. This phenomenon could be seen from the experimental and FEM results in the Figure 11. From 6% volume fraction content of diamond powder in the composite, there was a rapid increase in out of plane thermal conductivity and the steep increase remained until 12% volume fraction. Both measurement and FEM predicted this behaviour (Figure 11 and Table 6) which led to an increase in the out of plane thermal conductivity of up to 

4.4. Percolation and the Conductive Path Formation in the Composite
The formation of the conductive path and the interaction between filler-filler and fiber-filler could be further explained by the matrix percolation theory which refers to the onset of a sharp transition at which the cluster of conductive connectivity forms. The percolation theory [43] not only predicts a conductive network above the threshold, but also predicts near the percolation threshold where a steep increase in the thermal conductivity would be exhibited and this obeys the universal power scaling law near the threshold which are shown in the Equation (9), where the thermal conductivity of the matrix 

Figure 11. Comparison of the FEM and the experimental results of the diamond powder filled YS90A composite (50% fiber volume fraction).
Table 6. Out the of plane thermal conductivity of YS90A composite filled with the diamond powder.

Literature data suggests that, in the case of randomly dispersed spherical particles, an estimated theoretical value of the critical volume fraction of 
The ability of the composite to form the cluster of thermally conductive path are determined based on the distances and the interactions between the fiber-fiber and diamond filler-fiber. In order to find the increase in the conductive path for the FEM model, it would be necessary to determine the average distance between the neighboring fibers and diamond filler within the RVE. The FEM models for the YS90A composite were taken as a reference and the nearest neighbor distance distribution function based on the probability density function were formed to determine the short distance interaction between fiber-fiber and fiber-filler-fiber and also to determine whether the distance pattern shows some degree of clustering.
It could be seen from the Figure 13(a), the nearest neighbour distance of the numerically generated micro- structure of 50 vol% fiber and 6 vol% diamond powder shows a lower peak at a higher distance, while the nearest neighbour distance for the microstructure with 12 vol% diamond powder (Figure 13(b)) shows a higher peak at a shorter distance. For the microstructure with 12 vol% diamond powder, the nearest neighbour distances are very close to a peak as a result of clustering of diamond filler between the neighboring fibers. For a randomly generated microstructure as shown in the Figure 13(c), the heat conduction and the conductive chain formation are dominated by the fibers when they are in close contact with the neighboring fibers and the diamond powder filler influences as a catalyst to form additional conductive path when they are in close contact between the fibers.
To further emphasize the behavior of fiber-fiber interaction and fiber-diamond filler interaction, a periodic distribution of YS90A fibers within a RVE along with diamond powder (12% volume fraction) are shown in Figure 14. Even though it would be unrealistic to have a periodic distribution of fibers in the real composite, the behavior shown in the Figure 14 explains that when fibers are aligned in close thermal contact with the neighboring fibers and when the diamond fillers are between the fibers, then the heat conduction would be much higher than the randomly generated microstructures (Figure 13(c)). The significance of heat conduction remains sensitive to the distance between neighboring fibers and diamond powder. Physically this means that, if a better
Figure 12. FEM result for matrix percolation.


Figure 13. Nearest neighbor distance function for numerically generated microstructure for YS90A composite with diamond powder of 6 vol% (a) and 12 vol% (b), FEM model for conductive path formation in YS90A composite with diamond powder of 12 vol% (c).
Figure 14. An example of heat conduction in the YS90A diamond powder filled (12 vol%) composite with the periodic fiber distribution.
dispersion of diamond powder could be achieved the results would be further enhanced. For better dispersion, the size and the volume content of the diamond powder are important as it influences the viscosity of the resin. In terms of fabrication of the samples with the microscale diamond powder, the uniform dispersion was limited due to the high viscosity of the diamond filled resin and the samples had to be fabricated by the hand layup technique. The smaller the filler size, the larger the surface area and the percolation threshold would also be lower. By using this characteristics, diamond powder incorporated composites can show the thermal conduc- tivity enhancement even at lower concentrations.
5. Conclusion
In this investigation, the out of plane thermal conductivity of the standard modulus T300 and the high modulus YS90A woven composites were examined by FEM and thermal measurements. FEM investigations with the higher diamond powder contents showed the formation of the conductive path through the interaction with fibers which improved the thermal transport. Current experimental investigations by dispersing the diamond powder on the dry fabric showed that the out of plane thermal conductivity of the T300 composite increased by a factor of 2.3% for 55% fiber volume fraction-14% diamond powder volume fraction. Experimental investigation via the matrix modification technique showed that the out of plane thermal conductivity of the YS90A composite increased by a factor of 2.8 with 50% fiber volume fraction-12% diamond powder volume fraction. The results showed that the thermal conductivity of the composites depends significantly on the fiber and diamond powder filler volume fraction. The above improvement in the out of plane thermal conductivity using diamond powder can benefit several composite applications. To extend this research, further activities towards the thermal conductivity and mechanical properties of composites could be carried out with the nanodiamond filler as the smaller size particles have the characteristics of higher aspect ratio and a lower percolation threshold as they require fewer contacts and also could enhance the bonding behavior with the polymer. One of the other promis- ing solution under consideration is to use cyanate ester resin as it has a high Glass Transition Temperature (Tg), easy pre-cure at moderate temperature (125˚C - 135˚C) [45] and a low viscosity at the room temperature before curing [46] .
Acknowledgements
The authors would like to thank Mr.Uwe Schmitt (IVW, Kaiserslautern) for his contribution in this work towards preparation of samples. The authors would also like to acknowledge the European Commission Seventh Framework Program (Marie Curie Initial Training Network “TALENT”, Grant Agreement 289161) for funding this research.
Cite this paper
M. Srinivasan,P. Maettig,K. W. Glitza,B. Sanny,A. Schumacher,M. Duhovic,J. Schuster, (2016) Out of Plane Thermal Conductivity of Carbon Fiber Reinforced Composite Filled with Diamond Powder. Open Journal of Composite Materials,06,41-57. doi: 10.4236/ojcm.2016.62005
References
- 1. Seungjin, H. and Chung, D.D.L. (2011) Increasing the Through-Thickness Thermal Conductivity of Carbon Fiber Polymermatrix Composite by Curing Pressure Increase and Filler Incorporation. Composites Science and Technology, 71, 1944-1952. http://dx.doi.org/10.1016/j.compscitech.2011.09.011
- 2. Lyndon, E. and Philip, B. (2008) The CERN Large Hadron Collider: Accelerator and Experiments. Journal of Instrumentation, 3, S08001.
- 3. ATLAS Collaboration (2008) The ATLAS Experiment at the CERN Large Hadron Collider. Journal of Instrumentation, 3, S08003. http://dx.doi.org/10.1088/1748-0221/3/08/s08003
- 4. ATLAS Collaboration (2010) ATLAS Insertable B-Layer Technical Design Report. CERN-LHCC-2010-013. ATLAS- TDR-19.
- 5. Devendra, K. and Rangaswamy, T. (2012) Evaluation of Thermal Properties of E-Glass/Epoxy Composites Filled By Different Filler Materials. International Journal of Computational Engineering Research, 2, 1708-1714.
- 6. Srinivasan, M., Maettig, P., Glitza, K.W., Sanny, B. and Schumacher, A. (2014) Multiscale Calculation for Increasing the Thermal Conductivity of Carbon Fiber Composite with Diamond Powder. Proceedings of XLII International Summer School Conference Advanced Problems in Mechanics (APM 2014), 481-490.
- 7. Ahmad, H., Crocombe, A.D. and Smith, P.A. (2012) Physically Based Finite Element Strength Prediction in Notched Woven Laminates under Quasi-Static Loading. Plastics, Rubber and Composites, 42, 93-100. http://dx.doi.org/10.1179/1743289812Y.0000000038
- 8. Mallick, P.K. (1993) Fiber-Reinforced Composites-Materials, Manufacturing, and Design. Marcel Dekker Inc., New York.
- 9. University of Tennessee Space Institute. Carbon Fiber Production. http://www.utsi.edu/research/carbonfiber/cf.htm
- 10. Scott, E.P. and Beck, J.V. (1992) Estimation of Thermal Properties in Epoxy Matrix/Carbon Fiber Com-posite Materials. Journal of Composite Materials, 26, 132-149. http://dx.doi.org/10.1177/002199839202600109
- 11. Seungjin, H., Jan, T.L., Yasuhiro, Y. and Chung, D.D.L. (2008) Enhancing the Thermal Conductivity and Compressive Modulus of Carbon Fiber Polymermatrix Composites in the Through-Thickness Direction by Nanostructuring the Interlaminar Interface with Carbon Black. CARBON, 46, 1060-1071. http://dx.doi.org/10.1016/j.carbon.2008.03.023
- 12. Schuster, J., Heider, D., Sharp, K. and Glowania, M. (2008) Thermal Conductivities of Three-Dimensionally Woven Fabric Composites. Composites Science and Technology, 68, 2085-2091. http://dx.doi.org/10.1016/j.compscitech.2008.03.024
- 13. Hong, J.H., Park, D.W. and Shim, S.E. (2010) A Review on Thermal Conductivity of Polymer Composites Using Carbon-Based Fillers: Carbon Nanotubes and Carbon Fibers. Carbon Letters, 11, 347-356. http://dx.doi.org/10.5714/CL.2010.11.4.347
- 14. Song, S.H., Park, K.H., Kim, B.H., Choi, Y.W., Jun, G.H., Lee, D.J., Kong, B.S., Paik, K.W. and Jeon, S. (2013) En-hanced Thermal Conductivity of Epoxy-Graphene Composites by Using Non-Oxidized Graphene Flakes with Non-Covalent Functionalization. Advanced Materials, 25, 732-737. http://dx.doi.org/10.1002/adma.201202736
- 15. Cui, W., Du, F., Zhao, J., Zhang, W., Yang, Y., Xie, X. and Mai, Y. (2011) Improving Thermal Conductivity While Retaining High Electrical Resistivity of Epoxy Composites by Incorporating Silica-Coated Multi-Walled Carbon Nanotubes. Carbon, 49, 495-500. http://dx.doi.org/10.1016/j.carbon.2010.09.047
- 16. Fusao, H., Hiroyuki, K. and Yoshitaka, T. (2011) Synthesis of a Polymer Composite with Networked α-Alumina Fiber and Evaluation of Its Thermal Conductivity. Journal of the Ceramic Society of Japan, 119, 601-604. http://dx.doi.org/10.2109/jcersj2.119.601
- 17. Biercuk, M.J., Llaguno, M.C., Radosavljevic, M., Hyun, J.K. and Johnson, A.T. (2002) Carbon Nanotube Composites for Thermal Management. Applied Physics Letters, 80, 2767-2769. http://dx.doi.org/10.1063/1.1469696
- 18. Gordeye, S.A., Macedo, F.J., Ferrerira, J.A., van Hattum, F.W.J. and Bernardo, C.A. (2000) Transport Properties of Polymer-Vapor Grown Carbon Fiber Composites. Physica B: Condensed Matter, 279, 33-36. http://dx.doi.org/10.1016/S0921-4526(99)00660-2
- 19. Pierson, H.O. (1993) Handbook of Carbon, Graphite, Diamond and Fullerenes Properties, Processing and Applications. William Andrew Publishing, Noyes.
- 20. Yang, S., Lozano, K., Lomeli, A., Foltz, H.D. and Jones, R. (2005) Electromagnetic Interference Shielding Effectiveness of Carbon Nanofiber/LCP Composites. Composites Part A: Applied Science and Manufacturing, 36, 691-697. http://dx.doi.org/10.1016/j.compositesa.2004.07.009
- 21. Patton, R.D., Pittman Jr., C.U., Wang, L. and Hil, J.R.L. (1999) Vapor Grown Carbon Fiber Composites with Epoxy and Poly(phenylene sulfide) Matrices. Composites Part A: Applied Science and Manufacturing, 30, 1081-1091. http://dx.doi.org/10.1016/S1359-835X(99)00018-4
- 22. Xing, Y., Cao, W., Li, W., Chen, H., Wang, M., Wei, H., Hu, D., Chen, M. and Li, Q. (2015) Carbon Anotube/Cu Nanowires/Epoxy Composite Mats with Improved Thermal and Electrical Conductivity. Journal of Nanoscience and Nanotechnology, 15, 3265-3270. http://dx.doi.org/10.1166/jnn.2015.9677
- 23. Huang, H., Liu, C.H., Wu, Y. and Fan, S. (2005) Aligned Carbon Nanotube Films for Thermal Management. Advanced Materials, 17, 1652-1656. http://dx.doi.org/10.1002/adma.200500467
- 24. Koo, J.H. (2006) Polymer Nanocomposites: Processing, Characterization, and Applications. McGraw-Hill, New York.
- 25. Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Zhang, Y., Dubonos, S.V., Grigorieva, I.V. and Firsov, A.A. (2004) Electric Field Effect in Atomically Thin Carbon Films. Science, 306, 666-669. http://dx.doi.org/10.1126/science.1102896
- 26. Lee, C., Wei, X.D., Kysar, J.W. and Hone, J. (2008) Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science, 321, 385-388. http://dx.doi.org/10.1126/science.1157996
- 27. Balandin, A.A., Ghosh, S., Bao, W.Z., Calizo, I., Teweldebrhan, D., Miao, F. and Lau, C.N. (2008) Superior Thermal Conductivity of Single-Layer Graphene. Nano Letters, 8, 902-907. http://dx.doi.org/10.1021/nl0731872
- 28. Zhu, Y.W., Murali, S., Stoller, M.D., Ganesh, K.J., Cai, W.W., Ferreira, P.J., Pirkle, A., Wallace, R.M., Cychosz, K.A., Thommes, M., Su, D., Stach, E.A. and Ruoff, R.S. (2011) Carbon Based Super Capacitors Produced by Activation of Graphene. Science, 332, 1537-1541. http://dx.doi.org/10.1126/science.1200770
- 29. Stanford Advanced Materials. Advantages and Disadvantages of Graphene. https://samaterials.wordpress.com/2014/03/27/advantages-and-disadvantages-of-graphene/
- 30. Rakha, S.A., Khan, R.R., Khurram, A.A., Fayyaz, A., Zakaullah, M. and Munir, A. (2013) Mechanical Properties of Epoxy Composites with Low Content of Diamond Particles. Journal of Applied Polymer Science, 127, 4079-4085. http://dx.doi.org/10.1002/app.38029
- 31. Cytec Engineered Materials. Thornel T300 PAN-Based Fiber. Technical Data. https://www.cytec.com/sites/default/files/datasheets/THORNEL_T300_052112.pdf
- 32. Nippon Graphite Fiber Corporation. Pitch Based Carbon Fiber—GRANOC YARN YS-A Series. Technical Data. http://www.ngfworld.com/dcms_media/other/YSAfiber2014.pdf
- 33. N.N. (2013) Standard Test Method for Thermal Conductivity of Solids by Means of the Guarded-Comparative-Longi- tudinal Heat Flow Technique. ASTM E 1225-04.
- 34. Laubitz, M.J. (1984) Axial Heat Flow Methods of Measuring Thermal Conductivity. In: Cezairliyan, A., Maglic, K.D. and Peletsky, V.E., Eds., Compendium of Thermophysical Property Measurement Methods, Vol. 1, Plenum Press, New York and London, 11-59. http://dx.doi.org/10.1007/978-1-4615-6678-6_2
- 35. Sun, C.T. and Vaidya, R.S. (1996) Prediction of Composite Properties from a Representative Volume Element. Composites Science and Technology, 56, 171-179. http://dx.doi.org/10.1016/0266-3538(95)00141-7
- 36. Maligno, A.R., Warrior, N.A. and Long, A.C. (2009) Effects of Inter-Fiber Spacing on Damage Evolution in Unidirectional (UD) Fiber-Reinforced Composites. European Journal of Mechanics—A/Solids, 28, 768-776. http://dx.doi.org/10.1016/j.euromechsol.2008.10.009
- 37. Yang, L., Yan, Y., Ran, Z. and Liu, Y. (2013) A New Method for Generating Random Fiber Distributions for Fiber Reinforced Composites. Composites Science and Technology, 76, 14-20. http://dx.doi.org/10.1016/j.compscitech.2012.12.001
- 38. Math2Market GmbH. GeoDict for Composites. http://www.geodict.com/Solutions/Composites/Composites.php
- 39. e-Xstream Engineering. Digimat in Multi-Scale Analyses. http://www.e-xstream.com/products/digimat/technology
- 40. Melro, A.R., Camanho, P.P. and Pinho, S.T. (2008) Generation of Random Distribution of Fibers in Long-Fiber Reinforced Composites. Composites Science and Technology, 68, 2092-2102. http://dx.doi.org/10.1016/j.compscitech.2008.03.013
- 41. Dassault Systemes Simulia Corp. (2012) Abaqus Analysis User’s Manual, Version 6.12. Dassault Systemes, Providence.
- 42. Tu, S.T., Cai, W.Z., Yin, Y. and Ling, X. (2005) Numerical Simulation of Saturation Behavior of Physical Properties in Composites with Randomly Distributed Second-Phase. Journal of Composite Materials, 39, 617-631. http://dx.doi.org/10.1177/0021998305047263
- 43. Stauffer, D. and Aharony, A. (1991) Introduction to Percolation Theory. 2nd Edition, Taylor and Francis, London.
- 44. Scher, H. and Zallen, R. (1970) Critical Density in Percolation Processes. Journal of Chemical Physics, 53, 3759. http://dx.doi.org/10.1063/1.1674565
- 45. SAATI. Cyanate Ester Matrix. http://www.saati.com/images/composites/prepregs/ce662.pdf
- 46. Ament, K.A., Kessler, M.R. and Akinc, M. (2011) Cyanate Ester-Alumina Nanoparticle Suspensions: Effect of Alumina Concentration on Viscosity and Cure Behavior. Polymer Engineering & Science, 51, 1409-1417. http://dx.doi.org/10.1002/pen.21859
NOTES
*Corresponding author.













