ABSTRACT

Using the transfer matrix method we calculate the frequency dependence of the transmission of longitudinal elastic waves for a layered structure where the specific acoustic impedance of the layers with odd numbering follows a Gaussian distribution, while the inserted even layers have the same impedance as the propagation medium. The structure presents intervals of low-pass, band- stop, and band-pass. The characteristics of the bands depend on the number of layers, on the contrast between the maximum and minimum impedances of the structure, and on the ratio of the width of the inserted layers to the width of the layers with a Gaussian distribution of impedances.

Keywords:

Acoustic Transmission, Acoustic Impedance Modulation, Gaussian Profile

1. Introduction

Since many decades ago, the search for energy, electronic, optical and acoustic filters is an active field. In the area of acoustic, studies by Rayleigh opened an interest in the exploration of sound [1] . Pupins, Cambell and Wagner made the first studies to transmit information, where they proposed a transmission line and filtered the signals through simple configuration, known as T and π [2] [3] [4] . Later, the work development by Stewart in 1922 [5] [6] , began the study by acoustic filters. Stewart focused in the study on the relationship of the acoustic transmission between different media and applied the concepts of acoustic impedance, thus and analogy related to electrical circuits [7] [8] . Subsequently there was a series of works such as Peacock, Mason and Lindsay with which deepened and broadened the investigation of acoustic filters, then using the broad term studies of transmission line and varying conditions [9] - [14] . Today there extended literature on these issues. However, they have combined a group of applications, not only in acoustic but also in other research field, like signal processing, telecommunications, medicine, etc. [15] - [63] . In particular, there are proposals of energy band-pass filters using quantum superlattices with Gaussian potential profile [64] [65] . These structures allow the incident electrons to be nearly totally transmitted when the impinging energy is in the stop-band. The characteristics of the bands can be adjusted modifying the parameters of the superlattice and of Gaussian distribution. On the other hand, following the preceding idea, there is also a proposal of a multilayer optical structure where refractive index varies according to the envelope of Gaussian functions [66] . This structure acts as an omnidirectional mirror. For sound, the difference between acoustic impedance values between two media causes reflection at the interface. We propose in this work a multilayer acoustic filter where the specific acoustic impedance of the layers with odd numbering is modulated by a Gaussian functions. The acoustic impedance of the inserted provides a slow impedance for the layers, which can improve the transmission of the structure. We make a theoretical study of the transmission for this structure following a formalism of transfer matrix used for electromagnetic waves, which we have adapted to acoustic waves [67] . The 100% reflectivity and practically 100% transmission can be obtained when the frequency lies within the respective bands. The bands are flat and their positions and bandwidths are adjustable. This type of filter can be constructed experimentally using layers with composite materials where the acoustic impedance can be tailored by varying the volume fractions of the components in the composite [68] [69] . Another possible way to construct this filter is by using layers of porous silicon. This material has been widely used for the fabrication of optical devices, including optical filters where the refractive index can be varied through a variation of the porosity [66] . There are also studies of the variation of acoustical properties, including the acoustical impedance, due to the variation of the porosity [70] [71] . Recently, acoustic multilayer mirrors have been made using porous silicon [72] . In previous work, studies on acoustic, electronic and optical properties were made [73] [74] [75] . In this work we propose an alternative for generating acoustic filter from the modulation of the acoustic impedance and it is an effective method for making a better coupling of the acoustic impedances.

2. Theoretical Model and Calculation Method

For calculate the transmittance, we use the theory of references [67] [76] [77] . We consider a structure of N plane multilayers. The layers are perpendicular to the x axis. Each j-layers has a width d_j and acoustic Z_j given by

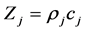(1)

where r_j and c_j, the density and the acoustic longitudinal speed for the j-materi- al, respectively. We consider longitudinal elastic plane waves propagating in the x-z plane, coming from left in a propagation medium with impedance Z_PM. The plane wave is incident on the structure of N plane multilayers. At the right side of the structure, the propagates in a medium PM with impedance Z_PM. We can write the wave function for each layer in the following form,

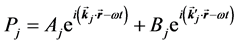(2)

where P_j presents the propagating wave pressure perturbation. The first and the second terms on the right-hand side Equation (2) represent propagation to the right and to the left, respectively, i.e. the forward and the backward waves. The index j = 0 represents the propagation medium at the left of the structure with impedance Z_PM. In the medium PM with j = N + 1 we consider only propagation to the right, consequently B_S = 0. k_j and 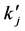are the forward and backward wave vectors for medium j, t is the time, ω the angular frequency, and i the imaginary unit. A solid can support both longitudinal and transverse elastic wave, and a fluid only transmits elastic longitudinal waves. If a longitudinal wave in a fluid is incident obliquely on the interface with a solid, both type of waves can be transmitted in the solid. However, at normal incidence, the character of the longitudinal wave is preserved, without generation of transverse wave in the solid. Then, for oblique incidence, our theory is valid only for fluid layers. If wave is incident at an angle θ₀ with the normal to the structure, law of Snell gives,

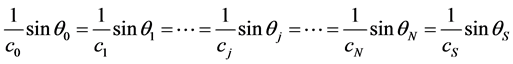(3)

The wave propagation from medium 0 to medium S through the multilayer structure is described propagation wave by,

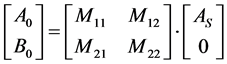(4)

where the (2X2) transfer matrix is given by [67] ,

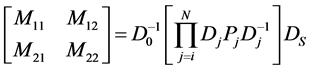(5)

The matrix D_j is called the dynamical or transmission matrix, and arises from the continuity conditions on the pressure and the displacement normal to the interface between media j-1 and j. The matrix P_j is the kinematical or propagation matrix inside the j layer. If it supposed that the media are lossless, the matrix are given by,

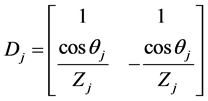(6)

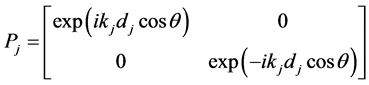(7)

where d_j is width layer in the structure. We define the transmission coefficient T as the transmitted power by the waves through the structure [78] , normal to the structure, divided by the power of the incident waves, normal to the structures. It is given in terms of the transfer matrix by,

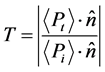(8)

where P_t is the vector of transmitted power, P_i the vector of incident power, and 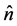the unit vector normal to the structure. The angle brackets denote average over time. P is similar to the Poynting vector in electromagnetism, which is given by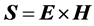, where 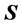is the vector of Poynting, 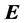is the vector of the electric field and 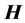is the vector of the magnetic field intensity, units are (W/m²). Similarly, the acoustic Poynting vector is given by, where 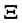is the acoustic Poynting vector, 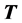is the stress to which the studied material is subjected and v is the particle velocity, the units of the acoustic Poynting vector are (W/m²) [79] . Its temporal average is given by [68] ,

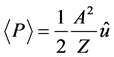(9)

here, A is the amplitude of the pressure wave and the unit vector in the direction of propagation of the wave. The transmission T, in terms of the transfer matrix, is given by,

(10)

The reflectance R is given by,

(11)

The specific acoustic impedance for the layers with odd numbers (Gaussian layers) in modulated by the Gaussian function,

(12)

where Z_max is the maximum impedance for the Gaussian values and Z_min is the impedance of the medium where the structure is situated, which is the same as the medium of the inserted even layers.

3. Results and Discussion

We consider that the structure is located in a propagation medium such as water, because later in the experimental stage, it can minimize signals or unwanted information (noise), compared to use in the air, as propagation medium. The following parameters are proposed with a minimum and maximum impedance. The proposed material is a composite, which has a range of minimum and maximum acoustic impedance, which are, Z₀ = Z_min = 1.509 MRayls, ρ₀ = ρ_min = 1000.0 kg/m³, c₀ = c_min = 1509.0 m/s, Z_max = 3.5 MRayl, ρ_max = 1500.0 kg/m³, c_max = 2333.0 m/s. The total thickness of the structure is fixed, with a value Δ = 1 in arbitrary units. For the Gaussian function, we use a value of σ = Δ/4, which for our calculations gives an efficient transmission. For the calculations, it is necessary to know for each value of Z calculated by Equation (12), the corresponding values of ρ and c for the Gaussian layers. For that purpose, we also make a Gaussian interpolation for ρ between the values of ρ_max and ρ_min, and find the corresponding values of c using Equation (1). The Gaussian layers have a width d_G and the inserted layers have a width d_I. The impedance profile of the structure is show schematically in Figure 1.

The spectrum of allowed frequencies for an acoustical multilayer structure consists of quasi-bands of discrete values of eigenfrequencies, separated by gaps or stop-bands, where there is no transmission of sound [80] .

We present in Figure 2 the transmittance for normal incidence for a structure with a total of 45 layers, where 23 follow the Gaussian profile, with three different values of the ratio d_I/d_G = 1, 3, 5 as a function of w_D/c_water, where c_water is the speed of sound for water, when the ratio d_I/d_G increases, there is better transmission in the pass-band, their width increases and size of the stop-bands decreases.

The reason of this improvement of the transmission, is that the fraction filled by Gaussian layers which have larger values of impedance than the water.

In Figure 3 we make a comparison of the transmission spectra between a structure with Gaussian profile of impedances and a structure with a regular profile, where the layers with odd numbers have constant value of impedance Z = 3.0 MRayls. The structure with regular profile of impedances has the expected gaps of frequencies (stop-bands) but it does not have flat pass-bands as the structure with Gaussian profile. The oscillations that occur in the transmission spectrum for the regular structure (a), correspond to the eigenfrequencies. We observe 23 oscillations in each quasi-band, which correspond to the 23 layers that have the Gaussian profile (b).

The transmission in the pass-bands for the structure with regular profile is poorer due to the more abrupt change of impedances. A structure with regular profile can work as an acoustic mirror, but it is bad as an acoustic filter.

In the Figure 4 we show the spectra of transmission for two structures with different number of layer. If we put more layers in the structure, the bands move upwards. This behaviour is similar to that of the quasi-bands of energies for an electron is a superlattice when the wells and barriers are narrower.

Also, the pass-bands are wider because the number of eigenfrequencies increases. At the same time, the reflectance for the stops-bands is improved due to

the fact that there are more layers with large impedance. We present in Figure 5 the transmittance for two values of Z_max = 3.5 y 7.5 MRayls. When the difference between Z_min and Z_max is larger, the pass-bands area narrower because there is a more abrupt change for the impedance of the Gaussian layers, which causes more reflection. We stress that the positions of the pass-bands and widths of the bands can be adjusted changing the parameters of the structure.

Finally in Figure 6 we show the transmittance of oblique incidence for four values of incidence angle (0, 45, 70 and 80) for the structure with 45 layers. When the angle of incidence increases the bands move towards intervals of higher frequencies and the transmission is poorer, as expected.

At the same time, the low-pass band becomes wider. About 80 the transmission practically disappears. We emphasize our calculations for oblique incidence is valid only for fluid layers.

4. Conclusions

Using a method of transfer matrix for electromagnetic waves, we have made studies in order to propose a layered acoustic filter where the characteristic impedance of the layers with odd numbers follows a Gaussian distribution and the inserted layers with even number have a constant value of acoustic impedance. Adjustable flat transmission bands and reflection bands are obtained by properly choosing the structure parameters, when a longitudinal plane wave of sound is incident on the layered structure, is practically transmitted totally if the frequency lies in a pass-band and fully reflected if the frequency lies in a stop-band. These properties have a wide area of application, such as in acoustic mirrors and filters. The latter allows to select specific frequency ranges to pass through them, for example in applications of medical ultrasound and the photoacoustic spectroscopy; also in the exploration and study of food to meet their properties and to apply the acoustic tools for food processing, as is the high intensity ultrasound.

Acknowledgements

R.A.R.V. acknowledges the support provided by Cátedras-CONACYT.

Cite this paper

Madrigal-Melchor, J., Enciso-Muñoz, A., Contreras-Solorio, D.A., Saldaña-Saldaña, X. and Reyes-Villagrana, R.A. (2017) A New Alternative Method for the Generation of Acoustic Filters, Modulating Acoustic Impedance: Theoretical Model. Open Journal of Acoustics, 7, 39-51. https://doi.org/10.4236/oja.2017.73005

References