Open Journal of Acoustics
Vol.06 No.01(2016), Article ID:65097,12 pages
10.4236/oja.2016.61001
Frequency and Energy Difference Detection of Dolphin Biosonar Signals Using a Decomposition Algorithm
Mark W. Muller
Department of Physics, Salisbury University, Salisbury, MD, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2016; accepted 26 March 2016; published 29 March 2016
ABSTRACT
A set of dolphin echolocation signals previously collected from an Atlantic bottlenose dolphin in Kaneohe Bay, Hawai’i are decomposed using a matching pursuit algorithm to further investigate the role of four types of echolocation signals outlined elsewhere [1] . The method decomposes the echolocation signals into optimal linear expansions of waveforms, which are Gabor functions defined in a dictionary. The method allows for study of the changes in frequency content within a dolphin’s functional bandwidth during discrimination tasks. We investigate the role of the functional bandwidth in terms of the signal energy levels and echolocations task performance. Furthermore, ROC analysis is applied to the relative energies of the matched waveforms to determine probability of discrimination. The results suggest that dolphins may discriminate by inspection of the relevant frequency differences between targets. In addition, the results from the ROC analysis provides insight into the role of the different classes of dolphin signals and of the importance of modification of the outgoing echolocation clicks, which may be fundamental to a dolphin’s ability to identify and discriminate targets.
Keywords:
Dolphin, Biosonar, Detection, Discrimination, Decomposition

1. Introduction
Using echolocation an Atlantic bottlenose dolphin, Tursiops truncatus, can make fine distinctions in the properties or features of targets such as size, shape, and material composition [2] [3] . The results of Au et al. [4] indicate that dolphins may have developed a unique way to process complex broadband transient sonar (acoustic) echoes for target discrimination. Traditionally, discrimination hypotheses have been developed by examining how dolphins may be using temporal or spectral cues in received echo signals for target discriminations. Dubrovskiy and Krasnov [5] suggested that dolphins discriminated spherical targets with different material compositions by difference in average oscillation period of the target echo frequency spectra. Au and Hammer [6] and Hammer and Au [7] proposed dolphins may use time separation pitch cues to discriminate targets. Au [3] hypothesized that the use of short-time frequency analysis may be a plausible method for target discrimination. Time-frequency analysis of dolphin echolocation signals provides a time-evolving representation of the signal frequency content as reported by Gaunaurd et al. [8] who used a Wigner-Ville representation. Muller et al. [1] reported that four classes of echolocation clicks are involved in the echolocation process of the Tursiops truncatus; moreover, the specific role of the different classes is not well understood. Although it may be possible for the dolphin to discriminate between time-frequency representations of different echolocation signals, it is difficult to quantify and detect subtle frequency and energy differences within a time frequency plot.
The matching pursuit algorithm decomposes a signal into a linear expansion of waveforms that are selected from a redundant dictionary of waveforms called time-frequency atoms [9] . By investigating the frequency content of the atoms, subtle frequency and energy differences between signals can be detected. Matching pursuit decomposition (MPD) [9] provides improved spectral resolution for time varying signals [10] and may be a useful tool for detecting subtle frequency differences in dolphin echolocation signals.
Previous studies have shown that matching pursuit decomposition is an effective method for detecting differences in signals. Gribonval and Bacry [11] used matching pursuit to decompose audio sound recordings with transient and sustained components and found matching pursuit to be an efficient method for detecting the individual components of the recording. MPD has also been shown to effectively detect frequency changes in a variety of biomedical signals [12] - [16] . Matching pursuit has not been previously applied to the decomposition of individual dolphin echolocation signals.
Dolphin echolocation signals are decomposed using matching pursuit to detect frequency and energy changes in the signals that may otherwise go undetected using traditional methods. The frequencies of the best matching waveforms (atoms) are investigated to determine subtle frequency changes of the echolocation signals. This provides novel insight into the frequency differences of the click and echo signals that are not readily revealed through Fourier or time-frequency representation methods. The results may provide an alternative method for investigation of dolphin sonar in terms of frequency and energy differences during echolocation and formulation of a discrimination strategy hypothesis.
Furthermore, receiver operating characteristic (ROC) analysis is utilized to evaluate overall detection and classification performances. ROC is a graphical analysis technique for binary classification systems with variable discrimination thresholds [17] . ROC curves have previously been used in detection studies involving marine mammal subjects and biomedical discrimination studies. Schusterman et al. [18] used ROC to show that the isosensitivity curves of the auditory detection sensitivity of marine mammals could be obtained by varying the response bias of the animals. Au and Turl [19] also used the technique of varying the response bias of an echolocating dolphin to obtain data that when plotted in ROC format could be fitted by an isosensitivity curve. In addition, Au and Pawloski [20] determined that the performance of an ideal receiver can be estimated by obtaining the isosensitivity curve that best fits the dolphin’s performance data plotted using a ROC curve.
2. Methods
2.1. Data Collection and Processing
The dolphin echolocation clicks were collected from previously described phantom echolocation experiments [21] . The subject used in the experiments was a 21-year-old female Tursiops truncatus named BJ. The animal was born in the laboratory and used in a variety of echolocation experiments [22] - [24] . The clicks were recorded by a Brüel and Kjaer 8103 hydrophone with a flat frequency response (±3 dB) up to 120 kHz. The recorded clicks were amplified and sent to a Measurement Computing Corporation PCI-DAS4020/12 analog to digital input board which digitized the signals at a sampling rate of 1 MHz. The clicks from both successful and non- successful discrimination trials were collected. The dolphin echolocation clicks were then clustered into four classes using spectral measurements and a clustering model based on the Bayesian Information Criterion [25] . The four classes are similar to those reported by Au et al. [26] and the characteristics of the classes are given elsewhere [1] . The echolocation clicks were incorporated into an acoustic scattering model [27] to obtain the echo signals for each click incident upon a steel, brass, iron, and lead spherical target of equal diameter. A detailed description of the click classification and the scattering model results are given by Muller et al. [1] . The echo signals from 400 incident clicks (100 from each class) are then decomposed by the matching pursuit algorithm.
2.2. Matching Pursuit Method
The matching pursuit decomposition is based on expanding a signal s(t) in the form of a linear expansion of waveforms xn from a dictionary of functions:
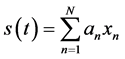 (1)
(1)
where the coefficients an are given by the inner products of the dictionary’s functions with the signal. In the first step of the procedure, the waveform xn which best matches the signal s(t) is chosen from a stochastic dictionary of normalized functions (|xn| = 1). The stochastic dictionary is generated before decomposition and consists of cosine packets [28] . In each of the consecutive steps, the waveform xn is matched to the residual signal Rns(t) by taking the inner product of the waveform xn and Rns(t) and multiplying by the waveform xn, which is the residual left after subtracting results of previous iterations:
 (2)
(2)
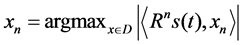
The waveform xn is chosen by the maximum absolute value of the inner product of the residual Rns(t) and the waveform xn. The procedure is repeated on the residual vector Rns(t) until the signal s(t) is decomposed into a series of time-frequency atoms in decreasing energy order. The frequency atoms which have a relative energy of 0.1 or higher after decomposition, which are denoted as the relevant atoms, are included in the post-processing analysis. The relevant atom data are presented in the form of time-frequency tile plots with shading indicating Heisenberg cells of atoms that make significant contributions to the signal. The intensity of the shading corresponds to the significance of the atom. The signals were decomposed using Wave Lab 850 [29] for MATLAB.
2.3. Functional Bandwidth
Ibsen [30] showed that for phantom echo signals, the dolphin utilizes frequencies between 29 and 42 kHz when performing discriminations, thus making the frequency band of 29 - 42 kHz her functional bandwidth. This was found by a discrimination experiment involving a stainless-steel phantom target as a standard stimulus. The comparison stimuli consisted of frequency filters applied to the standard stimulus to eliminate particular frequency bands from the standard phantom echo signal. The upper limit of the functional bandwidth corresponds with the animal’s upper frequency hearing limit of 45 kHz [30] . Since this is the only study to the author’s knowledge on determining a dolphin’s functional bandwidth, a direct comparison with other dolphins is not possible. Indeed the functional bandwidth of other dolphins could be different depending on the animal’s hearing abilities, echolocation strategies, and habitat. However, previous studies on the time frequency content of scattered dolphin waveforms did not examine this restriction [1] [8] . Each of the time-frequency tile plots of the atoms is truncated to indicate the relevant frequencies within animal’s functional bandwidth. This allows investigation of frequency changes and differences within the functional bandwidth and provides insight on the animal’s echolocation strategy.
2.4. Receiver Operating Characteristic Curves
ROC analysis is applied to the dolphin echolocation signals to provide insight on discrimination based on the relevant frequencies and corresponding relative energies of the signals. The atoms above the relative energy threshold of 0.1 are investigated in terms of frequency; all relevant atoms with frequencies not within the animal’s functional bandwidth are excluded from the computation. The relative energies of the remaining relevant atoms (atoms with frequencies within the functional bandwidth) are evaluated for each click. The relative energies from 100 clicks from each click class for each of the targets are then summed. The true positive and false positive rates between the positive class (standard target) and a negative class (comparison target) are calculated and plotted in ROC space. The steel sphere is used as the standard target as it has been traditionally used as the standard target in echolocation studies [21] [30] [31] .
In order to quantify the significance of the ROC curves, the area under the ROC curve (AUC) and corresponding p-values are calculated for each case. Green and Swets [17] showed that the AUC value corresponds to the probability of correctly identifying a standard stimulus from a comparison stimulus. The ROC curves and the AUC values are used here to determine if a comparison target can be identified from a standard target based on the relevant frequencies and corresponding relative energies of the dolphin echolocation signals. All ROC curves and AUC values presented were computed using a MATLAB toolkit [32] .
3. Results
An echo waveform from an echolocation click incident upon a spherical steel target and the corresponding time-frequency representation of the signal are displayed elsewhere [33] . Examples of cosine waveforms used in the dictionary for decomposition in decreasing matched energy and the echo signal reconstructed from the matched waveforms above the 0.1 threshold level is also displayed elsewhere [33] .
Figure 1 displays time-frequency tile plots of atoms after decomposition of each type of click incident upon a steel sphere. Figure 2 displays time-frequency tile plots of atoms after decomposition of each type of click incident upon a brass sphere. Figure 3 displays time-frequency tile plots of atoms after decomposition of each type of click incident upon an iron sphere. Figure 4 displays time-frequency tile plots of atoms after decomposition of each type of click incident upon a lead sphere. Each of the tile plots is band passed filtered to only include the animal’s functional bandwidth. The shading of the cells indicates the significance of the atom’s contribution to
Figure 1. Time-frequency tile plots of atoms after decomposition of (a) type I, (b) type II, (c) type III, and (d) type IV clicks incident upon a steel sphere. The intensity of the shading is proportional to the significance of the atom’s contribution to the signal.White indicates the least significance and black represents the highest significance. The dashed lines represent the functional bandwidth.
Figure 2. Time-frequency tile plots of atoms after decomposition of (a) type I, (b) type II, (c) type III, and (d) type IV clicks incident upon a brass sphere. The intensity of the shading is proportional to the significance of the atom’s contribution to the signal. White indicates the least significance and black represents the highest significance. The dashed lines represent the functional bandwidth.
Figure 3. Time-frequency tile plots of atoms after decomposition of (a) type I, (b) type II, (c) type III, and (d) type IV clicks incident upon an iron sphere. The intensity of the shading is proportional to the significance of the atom’s contribution to the signal.White indicates the least significance and black represents the highest significance. The dashed lines represent the functional bandwidth.
Figure 4. Time-frequency tile plots of atoms after decomposition of (a) type I, (b) type II, (c) type III, and (d) type IV clicks incident upon a lead sphere. The intensity of the shading is proportional to the significance of the atom’s contribution to the signal. White indicates the least significance and black represents the highest significance. The dashed lines represent the functional bandwidth.
the signal. The intensity of the shading corresponds to the relevance of the atom; the darker the shading, the more relevant an atom is to the contribution of the signal.
Upon inspection of Figure 1(a) there is a distinct dark cell followed by a less intense cell across the same frequencies. These cells may correspond to the primary and secondary highlights of the echo signal. Figure 1(b) displays four distinct cells; Figure 1(c) displays an initial cell followed by a longer duration cell, and Figure 1(d) contains only two distinct cells with the second cell having a lower intensity than the first. A comparison of the brass target to the steel target indicates that Figure 2(a), Figure 2(b) are similar to Figure 1(a), Figure 1(b). Upon investigation of Figure 2(c) and Figure 1(c), there appears to be a significant difference between the relevant atoms based on observation. Figure 2(d) is similar to Figure 1(d) however the intensities of the cells are reversed. A comparison of the iron target to the steel target indicates general similarities between the tile plots (Figure 1 and Figure 3) which is expected to certain extent due to the similar material properties of the two metals. The comparison between the steel target and the lead target again illustrates similarities between Figure 1(a), Figure 1(b) and Figure 4(a), Figure 4(b). Comparison of Figure 1(c), Figure 1(d) and Figure 4(c), Figure 4(d) indicates significant differences in the functional bandwidth. The lead target produces long duration single relevant frequencies as most of the frequency content of the echo is in a higher frequency range, outside of the functional bandwidth. The shading level of the Heisenberg cells provides a novel method to indicate frequency differences. Table 1 indicates the center frequencies of the matched waveforms displayed in the tile plots (Figures 1-4).
Figure 5 shows the ROC curves of relative energies of relevant atoms between a steel target and a brass target for 100 clicks from each class. Figure 6 shows the ROC curves of relative energies of relevant atoms between a steel target and an iron target for 100 clicks from each class. Figure 7 shows the ROC curves of relative energies of the relevant atoms between a steel target and a lead target for 100 clicks from each class. The dashed line in each of the plots represents the line of no discrimination. For each case, the ROC curve moves further away


Figure 5. ROC curves of relative energies of relevant atoms between a steel target and a brass target for (a) 100 class I clicks; (b) 100 class II clicks; (c) 100 class III clicks; and (d) 100 class IV clicks. The dashed line represents the line of no discrimination.
Table 1. Center frequencies in kHz of the matched waveforms (atoms) within the animal’s functional bandwidth. A blank means the center frequency of the matched waveform at that specific energy level is outside the animal’s functional bandwidth.


Figure 6. ROC curves of relative energies of relevant atoms between a steel target and an iron target for (a) 100 class I clicks; (b) 100 class II clicks; (c) 100 class III clicks; and (d) 100 class IV clicks. The dashed line represents the line of no discrimination.


Figure 7. ROC curves of relative energies of relevant atoms between a steel target and a lead target for (a) 100 class I clicks; (b) 100 class II clicks; (c) 100 class III clicks; and (d) 100 class IV clicks. The dashed line represents the line of no discrimination.
from the line of no discrimination as the average center frequency and rms bandwidth of the incident clicks are increased. The AUC values for each of the plots are given in Table 2 and the AUC values consistently increase for each of the cases as the average center frequency and rms bandwidth of the incident clicks are increased.
4. Discussion
The tile plots provide time-frequency representations of the relevant atoms and their respective contributions to the signal. This represents an improvement over the visual inspection of the time frequency plots presented earlier in [1] . Furthermore, in this study we examine the signal content within the animal’s functional bandwidth. Upon investigation of the time-frequency differences of the relevant atoms, the most significant energy differences occur near the limits of the animal’s functional bandwidth. For example, from visual inspection the steel and iron targets appear the most similar in terms of time-frequency characteristics. However, the tile plots reveal the largest energy differences from atoms centered at frequencies at 30 and 40 kHz. The energy differences occur for the same frequencies for all four types of clicks. However as the center frequency and bandwidth of the clicks increase, the differences become greater and thus more significant with the exception of the comparison of the class IV click incident upon the steel and iron spheres. It is difficult to distinguish the steel sphere from the iron sphere based on inspection of the RIDs of the class IV click (see [33] ). However, upon inspection of the MPD tile plots between these cases, the iron target exhibits a higher energy primary atom and an additional atom with a center frequency of 35 kHz which the steel target lacks (see Table 1). By examining this atom decomposition within the animal’s functional bandwidth better insight into discrimination methods might be developed as its ability to detect these differences is examined in future experiments.
Au et al. [4] suggested that during echolocation, dolphins perform like an energy detector with an integration time of approximately 264 μs. The auditory integration time is the temporal window over which a dolphin integrates an echo signal. The integration time was determined experimentally using a staircase procedure and multi-component signals with varying separation times. If the animal is behaving as an energy detector during echolocation, then it may be possible that the dolphin can detect the energy differences of the relevant atoms. These results support the hypothesis that if the animal is focusing on the relevant frequencies of the echo signal, the lower frequency, narrower band clicks may be used as search type clicks whereas the higher frequency, broader band clicks are utilized to ascertain more information about the target.
The ROC curves provide insight on the probability of discrimination based on the energies of the relevant atoms and role of the four different types of clicks. The results from the ROC analysis indicate that as the center frequency and the rms bandwidth of the incident clicks are increased, the probability of discrimination between targets is increased. The analysis was based on the relative energies of the corresponding relevant atoms. If the
Table 2. AUC values.
dolphin is monitoring the energy density of the received echo signals within her functional bandwidth, then it may be difficult to discriminate targets using only class I type clicks thus requiring a shift to higher frequencies. If this is the case, the class I clicks may be used to determine the location of a target and the clicks from classes II, III, and IV may be used to provide more information about the target to aid the animal during the discrimination task. The ROC results provide an explanation as to why the dolphin increases the rms bandwidth and center frequency of the incident clicks during discrimination tasks.
The results of this study show that significant frequency differences between various echolocation signals within a dolphin’s functional bandwidth can be extracted by the use of the matching pursuit algorithm. The MPD approach incorporates adaptive signal processing and atom decomposition which is advantageous in investigating the time-frequency content. Although subtle frequency differences can be discerned using MPD, the question remains whether the dolphin’s auditory system can detect this level of frequency differences. Herman and Arbeit [34] and Thompson and Herman [35] reported a dolphin could discriminate between a pure tone and a FM signal with at least a 1% difference limen across frequencies from 1 to 140 kHz. To best of the author’s knowledge there have been no experiments conducted in which a dolphin is asked to perform a frequency discrimination task using click-like signals though this appears to be a promising topic for further study. Moreover, it can only be hypothesized that these frequency differences may be detected and utilized by a dolphin during a discrimination task. A discrimination experiment might be designed using a phantom echolocation system which uses a standard target and comparison targets in which predetermined relevant frequencies are eliminated from the standard target. This type of experiment might quantify and determine the importance of relevant frequencies during a discrimination task and the frequency discrimination resolution of a dolphin’s clicks.
Acknowledgements
The author would like to thank Whitlow W. L. Au, Paul E. Nachtigall, and John S. Allen of the University of Hawai’i for their contributions to this work. The original data collected from the animal echolocation work was funded by the Office of Naval Research grant number 00014-098-1-687 to PEN and the support of Bob Gisiner and Jim Eckman are sincerely appreciated. The animal echolocation work was conducted under Marine Mammal Permit 978-1857-00 from the National Marine Fisheries Service (permit holder PEN) and authorized under University of Hawai’i IACUC Protocol number 93-005-15. The author would also like to thank the Richard A. Henson School of Science & Technology at Salisbury University for support of this project.
Cite this paper
Mark W. Muller, (2016) Frequency and Energy Difference Detection of Dolphin Biosonar Signals Using a Decomposition Algorithm. Open Journal of Acoustics,06,1-12. doi: 10.4236/oja.2016.61001
References
- 1. Muller, M.W., Allen, J.S., Au, W.W.L. and Nachtigall, P.E. (2008) Time-Frequency Analysis and Modeling of the Backscatter of Categorized Dolphin Echolocation Clicks for Target Discrimination. Journal of the Acoustical Society of America, 124, 657-666.
http://dx.doi.org/10.1121/1.2932060 - 2. Nachtigall, P.E. (1980) Odontocete Echolocation Performance on Object Size, Shape, and Material. In: Busnel, R.G. and Fish, J.F., Eds., Animal Sonar Systems, Plenum Press, New York.
http://dx.doi.org/10.1007/978-1-4684-7254-7_4 - 3. Au, W.W.L. (1993) The Sonar of Dolphins. Springer-Verlag, New York.
- 4. Au, W.W.L., Moore, P.W.B. and Pawloski, D.A. (1988) Detection of Complex Echoes in Noise by an Echolocating Dolphin. Journal of the Acoustical Society of America, 83, 662-668.
http://dx.doi.org/10.1121/1.396161 - 5. Dubrovskiy N.A. and Krasnov, O.S. (1971) Discrimination of Elastic Spheres According to Material and Size by the Bottlenose Dolphin. Acoustics Institute, Moscow, 17, 9-18.
- 6. Au, W.W.L. and Hammer, C.E. (1980) Target Recognition via Echolocation by Tursiops truncatus. In: Busnel, R.G. and Fish, J.F., Eds., Animal Sonar Systems, Plenum Press, New York, 855-858.
http://dx.doi.org/10.1007/978-1-4684-7254-7_40 - 7. Hammer, C.E. and Au, W.W.L. (1980) Porpoise Echo-Recognition: An Analysis of Controlling Target Characteristics. Journal of the Acoustical Society of America, 68, 1285-1293.
http://dx.doi.org/10.1121/1.385015 - 8. Gaunaurd, G.C., Brill, D., Huang, H., Moore, P.W.B. and Strifors, H.C. (1998) Signal Processing of the Echo Signatures Returned by Submerged Shells Insonified by Dolphin “Clicks:” Active classification. Journal of the Acoustical Society of America, 103, 1547-1557.
http://dx.doi.org/10.1121/1.421302 - 9. Mallatand, S.G. Zhang, Z. (1993) Matching Pursuits with Time-Frequency Dictionaries. IEEE Transactions on Signal Processing, 41, 3397-3415.
http://dx.doi.org/10.1109/78.258082 - 10. Akay, M. and Daubenspeck, J.A. (1999) Investigating the Contamination of Electroencephalograms by Facial Muscle Electromyographic Activity Using Matching Pursuit. Brain Lang, 66, 184-200.
http://dx.doi.org/10.1006/brln.1998.2030 - 11. Gribonval, R. and Bacry, E. (2003) Harmonic Decomposition of Audio Signals with Matching Pursuit. IEEE Transactions on Signal Processing, 51, 101-111.
http://dx.doi.org/10.1109/TSP.2002.806592 - 12. Bardonova, J. Provaznik, I. and Novakova, M. (2006) Matching Pursuit Decomposition for Detection of Frequency Changes in Experimental Data—Application to Heart Signal Recording Analysis. Scripta Medica, 79, 279-288.
- 13. Malinowska, U. Durka, P.J., Zygierwicz, J., Szelenberger, W. and Wakarow, A. (2007) Explicit Parameterization of Sleep EEG Transients. Computers in Biology and Medicine, 37, 534-541.
http://dx.doi.org/10.1016/j.compbiomed.2006.08.005 - 14. Sava, H., Pibarot, P. and Durand, L.G. (1998) Application of the Matching Pursuit Method for Structural Decomposition and Averaging of Phonocardiographic Signals. Medical & Biological Engineering & Computing, 36, 302-308.
http://dx.doi.org/10.1007/BF02522475 - 15. Zhang, X. and Durand, L.G. (1998) Analysis-Synthesis of the Phonocardiogram Based on the Matching Pursuit Method. IEEE Transactions on Biomedical Engineering, 45, 962-971.
http://dx.doi.org/10.1109/10.704865 - 16. Zhang, X., Durand, L.G., Senhadji, L., Lee, H.C. and Coatrieux, J.L. (1998) Time-Frequency Scaling Transformation of the Phonocardiogram Based on the Matching Pursuit Method. IEEE Transactions on Biomedical Engineering, 45, 972-979.
http://dx.doi.org/10.1109/10.704866 - 17. Green, D.M. and Swets, J.A. (1966) Signal Detection Theory and Psychophysics. Wiley, New York.
- 18. Schusterman, R.J., Barrett, R. and Moore, R.W.B. (1975) Detection of Underwater Signals by a California Sea Lion and a Bottlenose Porpoise: Variation in the Payoff Matrix. Journal of the Acoustical Society of America, 57, 1526-1532.
http://dx.doi.org/10.1121/1.380595 - 19. Au, W.W.L. and Turl, C.W. (1984) Dolphin Biosonar Detection in Clutter: Variation in the Payoff Matrix. Journal of the Acoustical Society of America, 76, 955-957.
http://dx.doi.org/10.1121/1.391279 - 20. Au, W.W.L. and Pawloski, D.A. (1989) A Comparison of Signal Detection between an Echolocating Dolphin and an Optimal Receiver. Journal of Computational Physiology A, 164, 451-458.
http://dx.doi.org/10.1007/BF00610439 - 21. Muller, M.W., Au, W.W.L., Nachtigall, P.E., Allen, J.S. and Breese, M. (2007) Phantom Echo Highlight Amplitude and Temporal Difference Resolutions of an Echolocating Dolphin, Tursiops truncatus. Journal of the Acoustical Society of America, 122, 2255-2262.
http://dx.doi.org/10.1121/1.2769973 - 22. Harley, H., Roitblat, H.L. and Nachtigall, P.E. (1997) Object Representation in the Bottlenosed Dolphin (Tursiops truncatus): Integration of Visual and Echoic Information. Journal of Experimental Psychology: Animal Behavior Processes, 22, 164-174.
http://dx.doi.org/10.1037/0097-7403.22.2.164 - 23. Aubauer, R., Au, W.W.L., Nachtigall, P.E., Pawloski, D.A. and DeLong, C.M. (2000) Classification of Electronically Generated Phantom Targets by an Atlantic Bottlenose Dolphin Tursiops truncatus. Journal of the Acoustical Society of America, 107, 2750-2754.
http://dx.doi.org/10.1121/1.428661 - 24. Ibsen, S.D., Au, W.W.L., Nachtigall, P.E., DeLong, C.M. and Breese, M. (2007) Changes in Signal Parameters over Time for an Echolocating Atlantic Bottlenose Dolphin Performing the Same Target Discrimination Task. Journal of the Acoustical Society of America, 122, 2446-2450.
http://dx.doi.org/10.1121/1.2772213 - 25. Schwarz, G. (1978) Estimating the Dimension of a Model. The Annals of Statistics, 6, 461-464.
http://dx.doi.org/10.1214/aos/1176344136 - 26. Au, W.W.L., Pawloski, J.L., Nachtigall, P.E., Blonz, M. and Gisner, R.C. (1995) Echolocation Signals and Transmission Beam Pattern of a False Killer Whale (Pseudorca crassidens). Journal of the Acoustical Society of America, 98, 51-59.
http://dx.doi.org/10.1121/1.413643 - 27. Brill, D., Gaunaurd, G., Strifors, H. and Wertman, W. (1991) Backscattering of Sound Pulses by Elastic Bodies Underwater. Applied Acoustics, 33, 87-107.
http://dx.doi.org/10.1016/0003-682X(91)90067-O - 28. Durka, P.J., Ircha, D. and Blinowska, K.J. (2001) Stochastic Time-Frequency Dictionaries for Matching Pursuit. IEEE Transactions on Signal Processing, 49, 507-510.
http://dx.doi.org/10.1109/78.905866 - 29. Donoho, D., Maleki, A. and Shahram, M. (2007) WaveLab 850. Department of Statistics, Stanford University, Stanford.
http://www-stat.stanford.edu/~wavelab/ - 30. Ibsen, S.D. (2006) Use of Phantom Echo Techniques to Determine Echolocation Parameters and Strategies of Dolphins. PhD Thesis, University of Hawai’i, Honolulu.
- 31. Aubauer, R. and Au, W.W.L. (1998) Phantom Echo Generation: A New Technique for Investigating Dolphin Echolocation. Journal of the Acoustical Society of America, 105, 1165-1170.
http://dx.doi.org/10.1121/1.424324 - 32. Fawcett, T. (2004) ROC Graphs: Notes and Practical Considerations for Researchers. Technical Report, HP Laboratories, Palo Alto.
- 33. Muller, M.W. (2008) Acoustic Modeling, Phantom Echolocation Experiments, and Time-Frequency Analysis of Dolphin Sonar for Improved Technological Sonar Systems. PhD Dissertation, University of Hawaii, Honolulu.
- 34. Herman, L.M. and Arbeit, W.R. (1972) Frequency Difference Limens in the Bottlenose Dolphin: 1-7 kc/s. Journal of Auditory Research, 12, 109-120.
- 35. Thompson, R.K.R. and Herman, L.M. (1975) Underwater Frequency Discrimination in the Bottlenosed Dolphin (1-140 kHz) and the Human (1-8 kHz). Journal of the Acoustical Society of America, 57, 943-948.
http://dx.doi.org/10.1121/1.380513












