Received 21 March 2015; accepted 18 May 2015; published 22 May 2015

ABSTRACT

Mixed models provide a wide range of applications including hierarchical modeling and longitudinal studies. The tests of variance component in mixed models have long been a methodological challenge because of its boundary conditions. It is well documented in literature that the traditional first-order methods: likelihood ratio statistic, Wald statistic and score statistic, provide an excessively conservative approximation to the null distribution. However, the magnitude of the conservativeness has not been thoroughly explored. In this paper, we propose a likelihood-based third-order method to the mixed models for testing the null hypothesis of zero and non-zero variance component. The proposed method dramatically improved the accuracy of the tests. Extensive simulations were carried out to demonstrate the accuracy of the proposed method in comparison with the standard first-order methods. The results show the conservativeness of the first order methods and the accuracy of the proposed method in approximating the p-values and confidence intervals even when the sample size is small.

Keywords:

Family Data, Genetic Variant, Likelihood Ratio Test, Random Effects, Third-Order Method, Variance Component

1. Introduction

Mixed models are a powerful tool with a wide range of applications including hierarchical modeling and longitudinal studies. In a variety of applied statistical problems, there is a need for inference on variance component, for example, the random effects ANOVA models, clustering [1] and homogeneity in stratified analyses [2] .

To introduce our ideas, we focus on a simple but generic setting of random intercept mixed model:

, (1)

where is the response for member 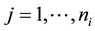of group, 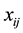is a vector of known covariates, 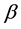is a vector of fixed effects, and is the group specific random effect, assumed to be independently distributed from the residual error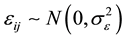. Assembling the into a vector Y and the rows into a fixed effect regressor matrix X, the marginal distribution of response Y is:

,

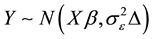in which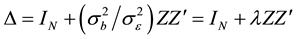, N is the total sample size and Z is the random effect regressor matrix. The parameter 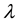can be considered as a signal-to-noise ratio since 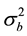determines the size of the “signal” given by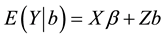. This is our parameter of interest.

The inference for variance component in mixed models has long been a methodological challenge because the variance component is restricted to nonnegative values, one typically needs one-sided tests of the null hypothesis especially when variance component is on the boundary, i.e.:

.

Using theory originally developed by Chernoff [3] , Liang and Self [4] and Stram and Lee [5] proved that the likelihood ratio test for testing a zero variance component has approximately a mixture distribution under the null hypothesis where represents a distribution with a point mass at 0. The p-value for the above one-sided test can be obtained from the mixture Chi-square distribution or equivalently from the standard normal distribution.

The restricted or residual maximum likelihood method (REML), proposed by Patterson and Thompson [6] , takes into account the loss of the degrees of freedom involved in estimating the fixed effects and reduces the downward bias of the maximum likelihood estimates of the variance component. However, simulation studies show that the likelihood ratio test based with the restricted maximum likelihood estimation is still conservative [7] .

In this paper, we consider the problem of testing the null hypothesis of zero and non-zero variance component in a linear mixed model and show the conservativeness of the first-order methods: likelihood ratio test, Wald test and score test. The likelihood-based third-order method by Fraser et al [8] is proposed to improve the accuracy of the inference. Our simulation studies show that the proposed method provides accurate approximation of p- values and confidence intervals even when the sample size is small. The likelihood ratio test approach performs much better than the Wald test and score test. One of the key contributions of this paper is that it gives the first detailed investigation of the accuracy of the tests of variance component in linear mixed models by various methods through extensive simulations with varying number of groups and group sizes.

We describe the general setting of the likelihood-based third-order method in Section 2. In Section 3, the method is applied to the random intercept model and then extended to the random intercept and random slope mixed model. We apply the methods discussed in this paper to a real data set from Genetic Analysis Workshop (GAW 18) in Section 4. Simulation results to compare the accuracy of the methods discussed in this paper are presented in Section 5. Section 6 provides a conclusion and discussion.

2. Likelihood-Based Third-Order Method

We consider inference for a scalar parameter of interest of a continuous statistical model with probability density function, in which θ is a vector parameter. Let be the observed log likelihood function. The two commonly used likelihood-based first-order methods are the Wald test and the signed log-likelihood ratio test. The Wald statistic for the parameter of interest is:

(2)

where, is the maximum likelihood estimate (MLE) of θ satisfying, is the hypothesized value of and is an approximated variance of, which can be obtained by the Delta method:

where

.

The Wald statistic follows asymptotically a standard normal distribution with first-order accuracy,. Hence the confidence interval for can be approximated by where is the th percentile of the standard normal distribution.

The signed log-likelihood ratio statistic takes the form:

(3)

where is the constrained maximum likelihood estimator of θ that maximizes subject to. Note that r also has a standard normal distribution with first-order accuracy. Hence, the confidence interval for is.

In recent years, various adjustments to the first-order methods have been proposed. In this paper, we consider the modified signed log-likelihood ratio statistic r^*, introduced by Barndorff-Nielsen [9] [10] , which takes the form

, (4)

where r is the signed log-likelihood ratio statistic as defined in Equation (3), and Q is a quantity that requires the existence of an ancillary statistic. When Q exists, Barndorff-Nielsen [9] [10] showed that r^* is asymptotically distributed as the standard normal distribution with third-order accuracy,. Hence, the confidence interval for is. However, it is well-known that the ancillary statistic may not exist, and even if it exists, it may not be unique.

Fraser et al. [8] presented a systematic method to obtain Q without requiring the existence of an ancillary statistic. More specifically, Fraser et al. [8] show that Q is the standardized maximum likelihood estimate departure calculated in the canonical parameter space. To obtain Q, all it requires is the observed likelihood function, and the parameter of interest. Let be the canonical parameter of an exponential family model. Then Q is a modification of q in Equation (2) that is calculated in scale, and it takes the form:

(5)

where is a re-calibrated scalar parameter on the scale obtained from the gradient vector of at the constrained maximum likelihood estimator:

.

Note that is the maximum likelihood departure calculated in scale. And is an estimated variance of, which takes the form:

, (6)

where

The subscripts indicate that the information has been recalibrated in terms of the new parameterization.

The canonical parameter of a model may not be explicitly available; however, Fraser and Reid [11] show that it can be approximated by

(7)

where V are the tangent vectors constructed using a vector of pivotal quantities:

. (8)

A simple and easy choice of V is given by the successive distribution functions, which are uniformly distributed. Thus, the quantity Q can be calculated by Equation (5) and p-value and the confidence interval for can be obtained from Equation (4).

3. Third-Order Method For Linear Mixed Models

In this section, we derive all the key equations of the first-order and third-order methods for the random intercept mixed model and the random intercept and random slope mixed model.

Third-Order Method for Random Intercept Mixed Model

Consider Model (1), the log-likelihood function can be written as

. (9)

The maximum likelihood estimates can be obtained from maximizing the log-likelihood

function (Equation (9)). For a fixed λ, the constrained maximum likelihood estimate of θ is. In

particular, and. Let. The Wald statistic q can be obtained by Equation (2) where the observed information matrix evaluated at is

where and are the first and second derivatives of.

The signed log-likelihood ratio statistic, r, defined in Equation (3) can be simplified to:

(10)

The constrained information matrix that will be used for the third-order method can be simply calculated by replacing in by the constrained maximum likelihood estimate.

The usual form of the score test statistic is given by

,

under the null hypothesis. Nuisance parameters are suppressed from notation. In the special case of testing zero variance component with, the score test statistic is ([12] ):

.

Similar to the signed likelihood ratio test statistic, the signed score test statistic is:

. (11)

Patterson and Thompson [6] proposed restricted or residual likelihood method which takes into account the loss of degrees of freedom involved in estimating the fixed effects and reduces the downward bias of maximum likelihood estimates of variance parameters. The restricted log-likelihood function is defined as

. (12)

The signed log-likelihood ratio statistic and Wald statistic with the restricted maximum likelihood can be obtained using the restricted log-likelihood function (Equation (12)) accordingly.

To obtain the third-order inference for λ, we need to find the canonical parameter. The canonical parameter is approximated by taking the sample space gradient at the observed data point in the directions of a set of vectors V (Equation (7)):

.

where the sample space gradient is

. (13)

Let. The tangent direction V is obtained from the pivotal quantity (Equation (8)):

. (14)

Let A denotes in Equation (14). Multiply Equations (13) and (14), we have the canonical pa-

rameter:

.

The Jacobian for is

.

Thus Q can be obtained by Equation (5) and we have the third-order approximations for λ by Equation (4). All the equations and the maximizing problems can be programmed into R.

4. Application: A Real Data Example

We use a data set from the Genetic Analysis Workshop (GAW 18) to illustrate the application of our proposed method. The Genetic Analysis Workshops (www.gaworkshop.org), which began in 1982, were initially motivated by the development and publication of several new algorithms for statistical genetic analysis, using different method of analysis. It is a collaborative effort among researchers worldwide to evaluate and compare statistical genetic methods, relevant to current analytical problems in genetic epidemiology and statistical genetics. The GAW 18 data set [13] was drawn from the San Antonio Family Study (SAFS) with a total of 959 participants from 20 families and it included the whole genome sequence data from all individuals. For each individual, age, sex, the use of hypertension diagnosis and antihypertensive medications (HTN) and tobacco smoking status (SMOKING) were recorded.

Our goal was to test the homogeneity of baseline systolic blood pressure (SBP) among families and if a genetic factor contributed to the variation of SBP among families. The test of homogeneity among families is a challenging task. The use of variance component of random effects in mixed models provides an efficient method to account for the heterogeneity among families.

4.1. Test of Homogeneity of SBP among Families

We first evaluated the homogeneity of SBP levels among families using a random intercept mixed model. We analysed the SBP levels with “AGE” as fixed effect in a random intercept mixed model accounting for the variabilities of SBP among families. A non-zero variance of random intercept implies there exists a significant variation of SBP levels among families and the group specific random intercepts allow us to identify the families that deviate the most from the population average SBP levels at baseline.

Let denote the SBP measurements for the ith individual in the jth family, the linear mixed model formula for GAW 18 data with random intercept can be written as

, (15)

where is the random intercept for the jth family.

To assess the variability of SBP, we obtain the 95% confidence interval of the variance component of random intercept λ. The 95% confidence intervals of λ obtained from third-order and first-order methods are recorded in Table 1. The third-order method yields a 95% confidence interval of containing no zero, suggesting a significant variation of SBP levels among families oppose to the results from first-order methods. The simulation studies have shown the superior accuracy of the third-order method and the conservativeness of the first-order methods. Thus we conclude that there is a significant variation of SBP among the 20 families based on the result from the third-order method. Figure 1(a) is the normal quantile plot of the random intercept for the 20 families. The normal quanitle plot also confirms the variability of SBP levels among families.

4.2. Test of Homogeneity of SBP among Families in Relation to a Genetic Factor

In a second step, we examine whether a combined genetic factor contributes to the variation of SBP levels among the 20 families using a random intercept and random slope mixed model. In a previous genome-wide association study (GWAS) from GAW 18 data, we showed that four single-nucleotide polymorphisms (SNPs) listed in Table 2 from different regions were associated with systolic blood pressure levels adjusting for demographical

variables [14] . We use the average number of minor alleles from these four casual SNPs for each individual (denoted as) was used as both as fixed effect and random slope in the model. To assess whether the effect of this combined genetic factor on SBP varies among families, we performed a test of variance component of the random slope in a random intercept and random slope mixed model. A non-zero variation of random slope implies significant variation of SBP levels among families due to the genetic factor. Backward elimination technique was used for model selection and led to the following random intercept and random slope mixed model:

(16)

where is the random intercept and is the random slope of the average number of minor alleles for the jth family and denotes the three-way interaction term including the lower order variables. The normal quantile plot of the random slope is shown in Figure 1(b) and displays substantial variability among families. The 95% confidence intervals of λ₁₁ obtained from third-order method, LRT-REML and LRT-ML are (0.1035, 1.1008), (0.0554, 1.0445) and (0.0457, 0.9658) respectively. Not surprisingly, result from the likelihood ratio test methods are more conservative than with the third-order method.

Our two sets of analysis therefore demonstrated the interest of the third-order approach, the only method to find significant heterogeneity among families in terms of baseline SNP and change of SPB due to a combined genetic factor.

5. Simulation Studies

In this section, we present results from simulation studies for the random intercept mixed model and random intercept and random slope mixed model to assess the improvement of the third-order method and examine the accuracy of the proposed third-order method compared to the following first-order methods:

1) Third-order: the third-order method based on maximum likelihood;

2) LRT-REML: the signed log-likelihood ratio statistic method with restricted maximum likelihood estimation;

3) LRT-ML: the signed log-likelihood ratio statistic method with maximum likelihood estimation;

4) Wald-REML: Wald statistic with restricted maximum likelihood estimation.

5) Wald-ML: Wald statistic with maximum likelihood estimation;

6) Score: Score test with maximum likelihood estimation.

The statistical software R (“nlme” package) was used to carry out all our analyses.

5.1. Simulation Results for the Random Intercept Mixed Model

We present simulation results for the null distribution of the zero variance component λ: versus and for non-zero variance component λ: versus in a random intercept mixed model.

5.1.1. versus

Balanced data sets with equal group size were generated with fixed effect, for the test of zero variance compoennt λ = 0. For each simulation configuration, 10,000 iterations were used for a number of groups m = 5, 10, 20, 50.

Probability-probability plots (pp-plot), similar to a quantile-quantile (qq-plot) but on the p-value scale rather than on the scale of the test statistic [6] , are used to examine the accuracy of the p-values obtained from the six methods. For a perfect approximation, the p-values line up on the 45˚ diagonal line. The nominal p-values calculated from the six methods, are plotted versus the empirical p-values in Figure 2(a). Figure 2(b) shows only the 0 to 15th percentile of Figure 2(a), that allows us have a clearer look at the differences. Figure 2 shows that when group size n = 10, the third-order method is surprisingly accurate and consistent regardless of the number of groups m. The likelihood ratio test is the most accurate among the first-order methods while the likelihood ratio test with restricted maximum likelihood estimation reduces the bias of maximum likelihood estimation. The approximations from Wald test and score test are poor, thus omitted for the rest of this paper. The figures also show that the proportion of point mass at 0 converges to 50% when sample size increases.

To further examine the accuracy of the third-order and first-order approximations, a 3-dimensional plot is used to visualize the bias for a number of groups m varying from 3 to 40 and group size n from 5 to 40 (Figure 3). The bias is calculated by subtracting the nominal p-value at the 5th percentile from its empirical (or true) p-value 0.05. A bias of zero implies perfect approximation and a positive bias implies conservativeness (greater than the true p-value). Figure 3 shows the same pattern as Figure 2: the third-order method is accurate and consistent. The likelihood ratio test with restricted maximum likelihood estimation is more accurate than that of maximum likelihood estimation. We observe an interesting pattern that is for a given number of groups m, the bias is small when the group size n is small, it increases with group size n and then flattens down and decreases slowly. For a given number of group size n, the bias decreases with m. The phenomenon suggests that the accuracy of first-order methods depend on both number of groups m and the group size n.

5.1.2. versus

In this section, we show simulation results for a non-zero variance component versus. Balanced data sets with equal group size were generated with fixed effect,

and λ = 4. For each simulation configuration, 10,000 iterations were used for a number of groups m = 5, 10, 20, 50. Again, the pp-plot in Figure 4 confirms the superior accuracy of the third-order method.

In addition, we examined the lower and upper error probabilities and the central coverage probabilities of third-order method and LRT methods. We generated data with m = 5, 10, 50 and n = 5, 10, 50 with 10,000 iterations for each configuration and recorded the coverage probabilities in Table 3. The performance of a method is assessed by the following values: the central coverage probability is the proportion of intervals that contains the true λ (CCP), the lower error probability is the proportion of true λ that falls outside the lower bound of the confidence interval (L) and the upper error probability which is the proportion of true λ that falls outside the upper bound of the confidence interval (U). The true CCP, L, and U are 0.95, 0.025 and 0.025 with standard errors

0.0022, 0.0016 and 0.0016, respectively. The table shows that the third-order method has the best coverage probabilities. It is always accurate with symmetric lower and upper error coverage probabilities. The LRT- REML has good central coverage probabilities in some cases however the lower and upper coverage probabilities are asymmetric with the lower error probabilities tends to be less than the true value and the upper probabilities tend to be larger.

5.2. Simulation Results for Random Intercept and Random Slope Mixed Model

Testing zero variance component of random slope in a random intercept and random slope mixed model implies that we are testing both λ₀₁ = 0 and λ₁₁ = 0. The third-order method is currently limited to the test of a scalar parameter. Theoretical development for vector parameter using third-order approach has not been proposed yet. Instead of testing λ₁₁ = 0, we could obtain the 95% confidence interval of λ₁₁. Thus we show the the simulation results for the test of a non-zero variance component of random slope versus. We generated balanced data sets with equal group size with fixed effect, , λ₀₀ = 1, λ₀₁ = 1 and λ₁₁ = 4, and a number of groups m = 5, 10, 20, 50. For each simulation configuration, iterations were used. Figure 5 is the pp-plot for versus. The third-order method has shown its superior accuracy and symmetric tail probabilities for the test of variance component of random slope in a random intercept and random slope mixed model. The LRT with REML is less conservative than LRT with ML.

In this section, we presented simulation results for the tests of variance component in linear mixed models. The simulation results demonstrated that the third-order method is accurate and consistent. The LRT method perform the best among all first-order methods and the REML reduce the bias comparing the ML. The computation time for third-order p-values is fast and depends on sample size. It takes only a few seconds for a sample of 40 group with group size of 40 on a personal computer with a Quad CPU @3 GHz and 8 GB RAM .

6. Discussion

A third-order likelihood-based method is proposed for the tests of zero and non-zero variance component in the random intercept mixed model and the random intercept and random slope mixed model. The third-order method requires only the observed likelihood function and derivation of the pivotal quantity and ancillary direction. The computation of third-order method is efficient. Our simulation studies show that the proposed third-order

likelihood-based method provides substantial improvement over traditional first-order methods. It provides extremely accurate and consistent approximation for the tests of variance component in mixed models even when the number of groups and group sizes are as small as five and three respectively. The likelihood ratio test performs the best among the first-order methods. The likelihood ratio test with restricted maximum likelihood estimation is less conservative than the maximum likelihood estimation. The likelihood ratio test with restricted maximum likelihood estimation is recommended for the test of variance component in mixed models whenever the first-order method is used. The application to the GAW 18 data illustrated the advantages of the third-order methods for the test of homogeneity among families in relation to a genetic factor. The simulation results also yielded a comprehensive evaluation of the accuracy of the first-order methods. The third-order method provides also opportunities for further applications in the context of longitudinal studies with repeated measurements and genetic studies. For example, there has been increased interest in genetic analysis to test the combined effect of several rare variants using random effects in the mixed model framework [14] . Since some popular approaches for this type of analysis are based on the score test of random effect, we think that the third-order approach could provide a more accurate alternative in this context, that we are planning to explore in future work.

Cite this paper

YanyanWu,AugustineWong,GeorgesMonette,LaurentBriollais, (2015) Evaluation of Third-Order Method for the Tests of Variance Component in Linear Mixed Models. Open Journal of Statistics,05,233-244. doi: 10.4236/ojs.2015.54025

References