Open Journal of Microphysics
Vol.07 No.04(2017), Article ID:81690,18 pages
10.4236/ojm.2017.74005
Experiments and Functional Realism
Edward MacKinnon
California State University, East Bay, Hayward, CA, USA
Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 30, 2017; Accepted: November 21, 2017; Published: November 24, 2017
ABSTRACT
This article focuses on interpreting theories when they are functioning in an ongoing investigation. The sustained search for a quark-gluon plasma serves as a prime example. The analysis treats the Standard Model of Particle Physics as an Effective Field Theory. Related effective theories functioning in different energy ranges can have different functional ontologies, or models of the reality treated. A functional ontology supplies a categorial framework that grounds and limits the language used in describing experiments and reporting results. The scope and limitations of such a local functional realism are evaluated.
Keywords:
Quark Gluon Plasma, Experimental Realism, Standard Model

1. Introduction
Wittgenstein revolutionized analytic philosophy by insisting that language should be studied when it is functioning, rather than when it is idling. He introduced the concept of a language game as a basic functioning unit for analysis. We will extend the Wittgensteinian approach by focusing on theories when they are functioning, rather than idling. The issue of realism enters in a functional way. What entities and properties are treated as real in experimental descriptive accounts? A clarification of this issue can then be related to the general problem of scientific realism.
A sketchy contrast with more traditional treatments of scientific realism highlights the distinctive features of the present approach. Philosophers have developed different ways of analyzing theories to determine their ontological import. Both the syntactic and the semantic approaches require the formulation of a theory as an uninterpreted mathematical formalism and then impose a physical interpretation through the denotation of basic terms in the axiomatic method, or through the imposition of models in the semantic method. This methodology requires that the abstract mathematical formulation has a consistency independent of the interpretation imposed on it. The ontology is essentially an answer to the question: “What must the world be like if this theory is true of it?” [1] [2] contrasts such foundational interpretations with “folklore” interpretations, where the folklore presumably stems from the physics community. In Wittgensteinian terms, a foundationalist interpretation is analyzing a theory when it is idling.
2. Quark-Gluon Plasma
We begin by analyzing an experimental program that has the double distinction of being the most extensive sustained experimental analysis performed by physicists and being the experimental program least analyzed by philosophers of physics. The experimental search for a quark-gluon plasma (QGP) has consumed more man-hours that any other experimental search in the history of physics, with the possible exception of the search for the Higgs particle. It is an attempt to clarify a phenomenon that is assumed to have played a decisive role in the formation of the universe. It also supplies a crucial test for the standard model of particle physics. Yet, to the best of my knowledge, it has not received any serious analysis from philosophers of science. I suspect that the major reason for this inadvertence is that the pertinent information is scattered through hundreds of technical articles stretching over more than two decades. It seems appropriate, accordingly, to present a non-technical summary before relating this to the theory-phenomenon interface.
Speculative accounts of the earliest phases of cosmic evolution suggest that after the inflation phase and the breakdown of both grand unification and electroweak unification there was a brief period where matter existed in the form of a quark gluon plasma (QGP). At about 10−8 seconds after the big bang, this plasma froze, or had a phase change, into hadronic matter: baryons and mesons. The phase change was a function of decreasing temperature and pressure.
The conditions that presumable led to the QGP can be reconstructed on a small scale with high-energy particle accelerators. A basic experiment is to accelerate two beams of heavy nuclei, usually gold or lead, in opposite directions and make them collide within a detector that can record decay products. A superficial account conveys the general idea. Quarks are confined within a nucleon. Because of the highly relativistic speeds colliding nuclei would be pancake shaped. Then there is sufficient overlap so confinement becomes meaningless. This should lead to a QGP. As this expands and cools, there is a phase transition from QGP to a shower of particles, which the detectors analyze.
The experimental attempts to produce and analyze a QGP started in 2000 with the Brookhaven Relativistic Heavy Ion Collider (RHIC) and were continued at the CERN Large Hadron Collider (LHC). In the RHIC experiments gold atoms are accelerated in steps through a van der Graaf accelerator, a Booster Synchroton, and an Alternating Gradient Synchrotron. These successively strip off electrons and finally inject completely ionized gold atoms into the RHIC storage rings.
Bunches of approximately 107 ions are accelerated in both clockwise and counter-clockwise directions and them made to collide within a detector with center of mass energies of up to 200 Gev. Only some nuclei collide. The working assumption is that there are grazing collisions between nuclei, grazing collisions between quarks, and some head-on collisions. Collisions between individual ions have energy densities corresponding to temperatures above 4 trillion degrees Kelvin. This is within the range of the temperatures calculated for the primordial QGP. It is assumed that these Au-Au collisions can lead to a phase transition from normal hadronic matter to a QGP state. Because of the extremely high temperatures and sharp localization the QGP would reach an equilibrium state in a very brief time. Chemical equilibrium obtains when all particle species are produced at the correct relative abundances. Kinetic equilibrium depends on temperature and flow velocity. This equilibrium only lasts for about 10−20 seconds. The following Figure 1 depicts the experimental situation:
The working assumption is that there is a four stage process. The earliest stage is dominated by high gluon density and the color-charge forces between them. This leads to the next stage, a glasma, a color glass condensate transverse to the beam direction that is not in equilibrium [3] . According to the Bjorken scenario, the transverse expansion continues until the transverse width is about the same as the longitudinal width and the plasma reaches an equilibrium condition. This occurs at a temperature of about 4 trillion degrees Kelvin and lasts about 10−22 seconds. The final stage is the transition to hadrons matter. Many of the particles formed decay immediately. Pions, kaons, protons, neutrons, photons, electrons, and muons from the transition or the decay processes travel freely until they reach the detectors.
The inferential process can be divided into two stages, computer inference and human inference. The computer inferences have two phases, analysis and reconstruction. The analysis of the debris products triggers the selection of events that match a priori criteria for specific types of events. This elicits a computer reconstruction of the event depicting the trajectories of hundreds of particles traversing powerful magnetic fields. The human inference concerns the analysis of these reconstructions. We will indicate how the detectors perform their analyses.
Both the RHIC and the LHC have four huge detectors with distinctive properties. I will simply indicate the basic structure of the detectors that specialize in QGP probes: the PHENIX and STAR detectors at RHIC and the ALICE and CMS detectors at LHC (See [4] , chap. 4). The typical form of a collider detector is a “cylindrical onion” containing four principal layers. A particle emerging from the collision and traveling outward will first encounter the inner tracking system, immersed in a uniform magnetic field, comprising an array of pixels and microstrip detectors. These measure precisely the trajectory of the spiraling charged particles and the curvature of their paths, revealing their momenta. The energies of particles are measured in the next two layers of the detector, the electromagnetic (em) and hadronic calorimeters. Electrons and photons will be stopped by the em calorimeter; jets will be stopped by both the em and hadronic calorimeters. The only known particles that penetrate beyond the hadronic calorimeter are muons and neutrinos. Muons, being charged particles, are tracked in dedicated muon chambers. Their momenta are also measured from the curvature of their paths in a magnetic field. Neutrinos escape detection, and their presence accounts for the missing energy.
Of the many questions these detectors treat we will only consider two that serve to illustrate the inferential systems involved. Was a QGP produced? Assuming a positive answer the next question concerns the nature of the QGP. The RHIC dominated attempts to answer the first question, while the LHC dominated attempts to answer the second. On the first question we will focus on one thread. If the production and decay of a QGP followed the scenario sketched, then the process should lead to the production of protons, kaons, and pions. If the high-energy collision did not lead to a QGP then the collision should lead to the production of protons, kaons, and pions. To detect the QGP production one must infer the distinctive features in particle abundances and fluctuations that the QGP would produce. However, fluctuations in the relative rates of hadron production are energy dependent and can be masked by other experimental effects.
The only reliable way to determine fluctuations is to analyze thousands of particle trajectories. Then one can compare ratios of protons to pions, and kaons to protons for different events [5] . Examining momenta presents further complications. If there is no QGP state then the shower of particles should have a Gaussian distribution proper to a gaseous state. Gases explode into a vacuum uniformly in all directions. If there is a QGP phase followed by particle freeze out, then particle distribution begins in a quasi-liquid state. Liquids flow violently along the short axis and gently along the long axis, or the axis set by the collider input. Statistically speaking, the difference between the two distributions would be characterized by kurtosis. Roughly speaking, kurtosis measures the width of the shoulders in a Gaussian type distribution curve. To work this out, e.g., for the distribution of proton transverse momenta, one needs enough individual event measurements to get a distribution curve, which can be compared with a Gaussian distribution.
The human inferential component centers on processing the thousands of computer reconstructions. The position paper outlining the analyses needed has some three hundred co-authors [6] . The data is farmed out to physicists all over the globe. A typical report coordinating their analyses will have a few hundred authors. One Physical Review letter reporting charged particle multiplicity density inferred from the CERN ALICE detector has 967 co-authors [5] . In 2005 a committee coordinating the results of different analyses wrote another three hundred co-author report concluding that the evidence for QGP formation was strong, but not definitive [7] . Within the next few years, with further supporting evidence, a consensus emerged that collider experiments did indeed produce a QGP.
Before considering the theories involved in these analyses we will return to the second question: What is the nature of a QGP? The initial assumption was that it should behave like a gas. Because of the asymptotic freedom of the strong force the quarks and gluons should behave as almost independent particles at the very small distances that obtain in a QGP. In 2003, [8] revived the hydrodynamic model that Landau had suggested in 1952. It led to the conclusion that the QGP may be the most perfect fluid known [9] . Two types of evidence supported this conclusion. The first came from an analysis of the momenta of particles in an event indicating more momentum transverse to the particle trajectory than along it. This was interpreted as elliptical flow characterizing a fluid. The second type of evidence came from jet quenching. Two sorts of events led to the production of particles with energies much larger than the energies of particles in the equilibria state of QGP. The first is a head-on collision of two quarks. They recoil with much higher energies than the thermal quarks. These high energy quarks loose energy through gluon emission and decay into a stream of secondary and tertiary particles, a jet. The second is the production of quarkonium due to the collision or decay of gluons.
Quarkonium is a quark-antiquark pair such as cc− (the J/ψ particle), or bb−, (the ϒ particle). Many other combinations are possible. Quarkonium has excited states similar to a hydrogen atom, 1s, 2s, 2p, 3s, 3p 3d. The energy they lose passing through a fluid depends on the state. Quarkonium also quickly breaks down into a shower of particles that strike the detectors. Selecting the particles that count as part of a jet and determining their energies presents formidable problems. There are competing algorithms to handle this problem. Proton-proton high energy collisions, which do not produce a QGP, also produce these two types of jets. An analysis of the differences between these two situations supplies a basis for inferring the quenching effects of the plasma.1
With the existence and basic properties of QGP established the experimental setup could be used to address further questions. We will consider one, measuring the decay of B-mesons. There are four types of B mesons all involving a bottom quark, b and an anti down, up, strange, or charmed quark: B0(bd−), B−(bu−), Bs(bs−), Bc(bc−). The decay of B mesons supplies a probe for physics beyond the Standard Model (SM). If new more massive particles not included in the SM exist, they must contribute to rare and CP-violating decays [6] [7] and a few hundred collaborators used results of the PHENIX detector to measure B meson decay. The details will be treated later.
3. The Framework of Experimental Analysis
Before analyzing the linguistic framework of the QGP experiments we will take a brief detour through the anti-Copenhagen Bohr. Bohr treated the contradictions quantum physics was encountering by introducing a Gestalt shift. Instead of discussing bodies with incompatible properties he analyzed the limits within which the classical concepts employed could function unambiguously. Before considering this analysis, we should attempt to dissipate the confusion resulting from the widespread identification of Bohr’s epistemology with the Copenhagen interpretation of quantum mechanics.
Bohr interpreted quantum physics as a rational generalization of classical physics, and classical physics as a conceptual extension of ordinary language ( [12] , Essay 1; [13] , chap. 3; [14] , pp. 131-138). He treated the mathematical formalism, not as a theory to be interpreted, but as a tool: “its physical content is exhausted by its power to formulate statistical laws governing observations obtained under conditions specified in plain language.” ( [12] , p. 12) Most contemporary physicists and philosophers of science would regard this way of interpreting quantum mechanics as bizarre. It is bizarre if one takes Bohr’s position as an interpretation of quantum theory. Bohr’s focus was on the information experiments, both actual and thought experiments, could provide. The pressing problem was that different experimental procedures relied on mutually incompatible descriptive accounts: electromagnetic radiation as continuous, X-ray radiation as discontinuous; atomic electrons traveling in elliptical orbits, an abandonment of this account in treating dispersion; electrons traveling in linear trajectories, electrons traveling as wave fronts. As the presiding figure in the atomic physics community, Bohr took on the problem of clarifying the conditions for the unambiguous communication of experimental information. This required considering the limits within which classical concepts can function without generating contradictions.
We should note that Bohr’s closest interpretative allies shared this view. Heisenberg declared: “・・・ the Copenhagen interpretation regards things and processes which are describable in terms of classical concepts, i.e., the actual, as the foundation of any physical interpretation.” ( [15] , p. 145) Pauli, Bohr’s closest ally on interpretative issues, contrasted Reichenbach’s attempt to formulate quantum mechanics as an axiomatic theory with his own interpretation: “Quantum mechanics is a much less radical procedure. It can be considered the minimum generalization of the classical theory which is necessary to reach a self-consistent description of micro-phenomena, in which the finiteness of the quantum of action is essential.” ( [16] , p. 1404)
Bohm’s 1952 paper on hidden variables effectively changed the status quaestionis [17] . He redeveloped the Schrödinger equation so that it supported a hidden variable interpretation. This induced an interpretative shift from the practice of quantum mechanics to the formalism. If the mathematical formulation of QM could support different interpretations, then particular interpretations required justification. Heisenberg ( [15] , chap VIII) joined the fray, presenting Copenhagen as an interpretation of the theory of QM. In this context, the Copenhagen interpretation, and Bohr’s epistemological reflections, were treated as interpretations of QM as a theory. Bohr never held or defended the Copenhagen interpretation of quantum mechanics. We will rely on Bohr’s original position.
Bohr’s insistence that any experiment in which the quantum of action is significant must be regarded as an epistemologically irreducible unit led to a restriction on the use of “phenomenon”. An unambiguous account of a quantum phenomenon must include a description of all the relevant features of the experimental arrangement. “・・・ all departures from common language and ordinary logic are entirely avoided by reserving the word ‘phenomenon’ solely for reference to unambiguously communicable information in the account of which the word ‘measurement’ is used in its plain meaning of standardized comparison.” [12] , p. 5)
We will replace Bohr’s “phenomenon” by Wittgenstein’s “language game”. Each experimental context must be treated as an irreducible language game. Bohr insists on a reliance on “plain language” in describing an experiment and reporting the results. MacKinnon [13] clarified this plain language requirement through an historical and conceptual analysis of the development of the extended ordinary language (EOL) used in physics. An experimental account is presented in an ordinary language framework augmented by the incorporation of physical terms. This requirement applies to both classical and quantum experiments. The difference between the two is not in the language game used, but in the relation between this language game and language games used for related experiments. In classical experiments they may be joined together in a larger account. In quantum experiments they often have a relation of complementarity.
Bohr illustrated this by presenting idealized accounts of single and double-slit experiments. We will replace this idealized account by an actual experimental program from the same era. In 1919 Davisson initiated a series of experiments scattering electrons off a nickel target. His goal was to determine how the energies of scattered electrons relate to the energies of incident electrons. Established physics supplied a basis for a coherent account of this phenomenon. He accepted the value of 10−13 as this size of an electron. Using this as a unit, the size of the nickel atom is 105 and the least distance between nickel atoms is 2.5 × 105. These values supported the presumption that individual electrons easily pass between atoms, but may eventually strike an inner atom and recoil. So, scattered electrons should have a random distribution.
This research project was interrupted when the vacuum tube containing the nickel target cracked. To eliminate impurities Davisson baked the nickel and then slowly cooled it. When he resumed his experiments the scattered electrons had something like a diffraction pattern. This indicated that individual electrons were scattered off the face of the target in much the ways X-rays are scattered off crystals. If he followed his earlier account, he would have to give a different account of the phenomenon of electron scattering. An electron has a collision cross-section of 1 when scattered off the original nickel and a collision cross-section of about 250,000 when scattered off the cleansed nickel. There is no coherent way in which one can join together two accounts of the same process of electron scattering where the particle size changes by a factor of 250,000, because the target is polished.
Davisson sent his results to Born and, following his advice, related the new results to the de Broglie formula for treating particles as waves: λ = h/p. Davisson, with the assistance of Germer, initiated a new set of experiments. They assumed that heating and cooling the nickel changed it into a collection of small crystals of the face-centered cubic type. This would support resonant scattering for certain voltages. For 54 volts Davisson’s calculations indicated an effective wave length of λ = 1.65 × 10−8 cm. The de Broglie formula yielded a wave length of λ = 1.67 × 10−8 cm. There was a similar correspondence at other resonant voltages [18] . This is a different, complementary, language game in which the electron is represented as a wave with a relatively long wave length.
An insistence that the linguistic framework for the QGP experiments is extended ordinary language may seem bizarre. The experiments are concerned with quarks, gluons, quark gluon plasmas, quarkonium, B mesons, J/ψ mesons and other “theoretical entities”. The Bohrian analysis, however, was not based on the terms used in the experimental account, but on the necessary conditions for the unambiguous communication of experimental information. This requirement is crucial for the experiments considered. The experimental analyses depend on the coordinated efforts of thousands of people scattered around the globe who communicate chiefly through internet correspondence. A typical report features a few hundred coauthors, most of whom never meet or talk to their coauthors. This is a recipe for confusion, not coherence. To present a coherent account all potential sources of ambiguity must be removed.
To see how this is done we will consider the two chief sources of potential failures in communication: the dialog between theoreticians and experimentalists; and the intercommunication between RHIC and a world-wide net of collaborators. For a theoretician, any interaction between two fermions is mediated by a virtual boson. Strong interactions are mediated by 8 types of gluons; weak interactions, including decays, by W+, W−, and Z bosons. Any experimental test of such interactions hinges on results that can be recorded and communicated. The mediating bosons are not recorded, because they are virtual particles. A classical example of theoretical-experimental dialog concerning the testing of particle predictions is the dialog between Gell-Mann and Samios. After Gell-Mann made the prediction of the Ω− particle at the 1962 CERN conference, he had a discussion with Nicholas Samios, who directed high-energy experiments at Brookhaven. Gell-Mann wrote on a paper napkin the preferred production reaction.
If a Ξ− had been produced, there would be a straight-line trajectory between its production point (the origin of the K+ track) and the vertex of the p → π− tracks. If a Ω− is produced there is a slight displacement due to the intermediate steps indicated above ( [19] , p. 533). Samios and his Brookhaven team began the experimental search, developed thousands of bubble-chamber photographs, and even trained Long Island housewives to examine the photos for the slight deflection inferred in the production of a Ω−. On plate 97,025, they finally produced a photograph that Samios interpreted as the detection of the Ω−. A copy of this photo adorns the paper cover of Johnson’s biography of Gell-Mann [20] . What the experiment produced and interpreted were classical particle trajectories.
The detection of B meson decay from the RHIC experiments presented formidable problems in theoretical/experimental coordination. The list posted by The Particle Data Group lists hundreds of particle decays for B mesons. The collaboration must select a decay process that has a relatively high probability and leads to results that can be detected by the PHENIX detector. The process selected for testing was B0 → J/ψ → µ+ + µ−. The data for testing this came from two different types of computer processed data. Figure 2 illustrates typical results of computer processing. The pictures shown are not obtained from B meson tests. They simply illustrate the computer processing. Figure 2(a) is the result of fast processing that provides the raw data on a collision. The blue lines indicate parts of the detector. The other lines are reconstructed tracks colored to indicate momenta: blue low; green, yellow intermediate; red high. This raw data is then processed by the RHIC computing facility that converts it into data that can be used for data analysis. Figure 2(b) is a simple example of event reconstruction of a deuteron + gold collision. The uniformly colored areas indicate different sections of the PHENIX detector. The sphere in the center is the collision vertex. The lines are projections whose colors indicate momentum. The length of the white spikes registers energy.


The Gell-Mann/Samios methodology could infer particle production from gaps in the bubble-chamber photographs. That method does not work when one is processing computer reconstructions, rather than photos. The key to detecting this decay process was the recording of paired muon tracks with the right energy. Recording this involves a nested series of triggers. This produces the data to be analyzed, a picture with a series of tracks and dots. A run can yield hundreds of such reconstructed pictures. Each requires a detailed analysis to determine the type of event recorded. This analysis is performed in hundreds of universities and research institutions across the globe.
This introduces the second area presenting difficulties in unambiguous communication, the interaction between RHIC and widely scattered analysts. There is a standard method for achieving uniform processing. Physics departments who wish to participate in this project receive a set of instructions and video tutorials. The tutorials teach the analysts how to use the software RHIC supplies to process the pictures RHIC supplies. A coordinator, usually a physicist at RHIC, puts the results together and produces a report listing a few hundred co-authors and the results of their analyses.
4. Effective Field Theory and Functional Ontology
The survey of QGP experiments involved a consideration of theories when they are functioning as tools, rather than when they are idling. The goal is to establish the existence and discover the nature of entities and processes postulated on theoretical grounds. This is broadly ontological. The overarching theory making the predictions and interpreting the experimental results is the Standard Model of particle physics (SM).2 The SM does not meet the standards philosophers set for theory formulation. The SM patches together three separate pieces treating weak, electromagnetic, and strong interactions. It does not have a mathematical justification independent of a physical interpretation. Instead, it relies on some sloppy mathematics, such as series expansions which have not been shown to, and probably do not, converge. It looks more like an ugly set of rules than a properly formulated theory. In spite of, or perhaps because of, these philosophical shortcomings it is the most successful theory in the history of physics. It supplies a basis for treating with depth and precision all the presently known particles and their interactions. This supplies a basis for atomic and molecular physics and chemistry.
Following the practice of physicists we will treat the SM as an Effective Field Theory (EFT), rather than a mathematical formulation on which one imposes a physical interpretation. To bring out the significance of this categorization, I will present a brief non-technical account of EFTs and then consider the extension to theories that are not field theories.3 The key idea of EFTs is to separate low energy, relatively long-range interactions from high energy, relatively short-range, interactions. An EFT treats the low energy interactions and includes the high-energy interactions as perturbations. We assume that there is a high energy, M, characterizing, for example, the mass-energy of a basic particle and lower energies, characterizing the interactions of interest. Between these energies a cutoff, Λ, is introduced, where Λ < M. We divide the field frequencies into low- and high-frequency modes, and use natural units (h− = 1 = c).
where φL contains the frequencies, ω < Λ. The φL supply the basis for describing low-energy interactions. EFT is similar to regularization and renormalization in eliminating high-energy contributions and then compensating for the effect of the elimination. Renormalization methods clarify the nature of this compensation. The high frequency contributions have the effect of modifying the coupling constants. Since the low-energy theory relies on experimental values for these constants, EFT gives no direct information about the neglected high-energy physics.
However, the renormalization group methods supply a basis for indirect inferences. One can introduce a new cutoff, Λc < Λ. A comparison of the calculations made with the two cutoffs supplies a basis for determining the variation of the coupling constants (no longer treated as constants) with energy.
Before considering an application of EFT we should consider its purported shortcomings. The reliance on sloppy mathematics is justified on physical, rather than mathematical, grounds. The higher order terms in the series expansions refer to higher energy levels than those treated by the EFT. This should be filled in by a new physics proper to the higher energy levels. EFTs support a kind of linguistic ontology. Instead of asking what the world must be like if the theory is true of it, it asks what sort of descriptive account fits reality at then energy level considered. This reliance on language signals that it is treating reportables, rather than beables.
The application of EFT methods to high energy particle physics involves a detailed consideration of the particular problems being treated, a very complex affair. We can illustrate the methodology by using it for a simple example where EFT methods are not needed. Besides illustrating the methodology the example supplies a model for a case where EFT methods are needed. The example is Fermi’s 1932 treatment of beta decay. To update it we will represent it by a Feynman diagram, Figure 3(a):

Figure 3(a)
Since this is a point interaction, it is not renormalizable. With retrospective hindsight one might regard Fermi’s account as an Effective Theory applicable for energies around the energy of beta decay, approximately 10 Mev. We take as a tentative cutoff, 940 Mev, roughly the mass energy of a neutron or proton. In a field theory approach we assume that the transition is mediated by some sort of boson. This is something belonging to a higher energy level which we contemporaries of Fermi do not know. So we assume that it is characterized by high frequency terms, which have effectively been integrated out and yield the coupling constant known from experiments. This leads to a revised Feynman diagram, Figure 3(b):

Figure 3(b)
The circle indicates the high frequency terms that have been in integrated out. A rough estimate is that it should introduce a correction term of order (10 Mev/ 940 Mev), about 1%. The time of the interaction is extremely short. So, a crude application of the indeterminacy relation, ∇E∇t ≥ h−, suggests that the mediating boson could have a high energy much greater than the rest mass energy of the neutron.
This can be compared with the account available after electroweak unification was established:
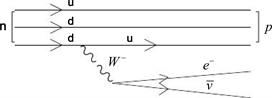
The W− meson, with a mass of 8.4 Gev, is in a higher-order energy range.
5. Effective Theories and Extended Language
The concept of effective field theories can be extended to Effective Theories (ET) that are not field theories. Thus Kane ( [29] , chap. 3) interprets physics in terms of a tower of effective theories. Rohrlich [30] treats the replacement of superseded by superseding theories for different energy ranges and analyzes the differences between the two in terms of functional ontologies and related semantics. For present purposes we will focus on one aspect of ETS, their effect on shaping the extension of ordinary language when a theory is employed in experimental contexts. We will indicate how this works in two simpler cases before returning to the QGP experiments. The first example is the treatment of light. A Kuhnian scenario suggests a sequence of paradigm replacements: Newton’s corpuscular theory, a wave theory, the semi-classical treatment of radiation used in non-relativistic quantum mechanics, and quantum electrodynamics. Since the “replaced” theories are still functioning, we will treat this as a succession of superseding effective theories and inquire how each may still be used.
The applicability of effective theories is set by the energy level treated. All treatments of visible light treat the same energy levels. The pertinent issue here is the energy range proper to the experimental arrangement. The energy level of light is set by its frequency, or inversely by the wave length of the light. Red light has a wave length around 7 × 104 mm. A slit one mm in width could accommodate over 1000 wave lengths. Under these conditions, it is appropriate to use the geometric optics that treats light as corpuscles traveling in straight-line rays. This geometric optics is still used in the design of cameras, microscopes, telescopes, and optometry. Fuzzy shadows and chromatic aberrations in telescopes would be regarded as phenomena requiring a higher level effective theory.
The interpretation of light as wave propagation is appropriate when the pertinent distances are comparable to the wavelengths involved. Consider the 1 mm slit again. Interference is explained by considering the interaction between light passing through a narrow portion of the slit and an adjoining narrow portion. A typical diffraction grating would have 100 lines per mm. So the separation between lines is comparable to the wavelengths of visible light, 3.8 - 7 × 104 mm. It is appropriate to speak of light as waves when treating interference, diffraction, interferometers, chromatic aberration, and fuzzy shadows. In quantum mechanics, one speaks of light as photons and uses this in descriptive accounts of laser beams. In each case, the language used to describe experiments and report results must be regarded as an extension of an ordinary language framework. One speaks not only of light, but also of the instruments, interactions, and human interventions involved. In the context of describing experiments and reporting results, these can be considered three different language games.
The second example will be treated more briefly. Chemists routinely rely on descriptive accounts of the size and shape of atoms and molecules. Such accounts are crucial in the treatment of large complex molecules.4 Quantum mechanical account of atoms do not support such size and shape attributions. As Figure 4 indicates, this difference can be interpreted in terms of effective theories operating at different energy levels. Further examples are treated in [30] : Newtonian mechanics for low energies and relativistic mechanics for velocities

Figure 4(b)
comparable to the velocity of light; Newtonian gravitational theory relying on forces and Einsteinian gravitational theory relying on curved space; liquid as a continuous fluid and liquid as a collection of molecules. The differing energy ranges are shown in Figure 4.
With the background, we return to the QGP experiments. As indicated earlier, the experimental analyses use different theories as tools. However, the guiding theory for the whole enterprise is the Standard Model of Particle Physics. The language used in describing experiments and reporting results includes the particles and processes systematized or predicted by the SM. There is no distinction between observables and theoretical entities. A descriptive account treats the accelerators, detectors, particles, interactions, and decays as objectively real. As logician has shown if a system contains a contradiction then anything follows. The language used must have the functional coherence requisite for avoiding contradictions. The coherence required is the coherence of a language game, not a formal theory. Since ordinary language presupposes a functional ontology of localized spatio-temporal objects with properties it treats both the particles involved and the detectors that record particle events as localized objects. This reliance on a functional ontology and the language it supports is justified on pragmatic grounds. It works.
These considerations can generate two different types of philosophical reactions. The first stems from taking isolated theories, rather than theories as used in experimental practice, as the basis of interpretation. Relativistic quantum mechanics does not support the non-relativistic position operator, . The effective position operator resulting from the Newton-Wigner or Foldy-Wouthuysen reduction of the Dirac wave function is a non-relativistic operator that smears position over a volume about the size of the particle’s Compton wavelength. Algebraic quantum field theory (AQFT) does not support a particle interpretation. What is the pragmatic significance of these objections? If AQFT were accepted as the ultimate science of physical reality then it would make sense to try to derive an ontology from the indispensable presuppositions of the theory. However, AQFT cannot handle the interactions treated in the SM, which is an effective, not an ultimate theory. If AQFT is regarded as an idealization of functioning quantum field theory then a clarification of its ontological significance sets constraints on the interpretation of field theories. It does not tell us what the world must be like if AQFT is true of it.
A different philosophical approach would ask which aspects of the descriptive account are determined by the language game used rather than the reality treated. In the Davisson example the original reporting relied on a language game in which electrons were spoken of as small particles traveling in trajectories. A coherent account of the revised experiments using the polished nickel crystal required a switch to a language game in which electrons were spoken of as waves, with wavelengths 250,000 times the size of the “particle” electron, that can diffract and interfere. Here it is reasonable to conclude that the talk of localized particles is a feature of the language game imposed, not an intrinsic feature of the reality treated.
A similar switch is not pragmatically feasible in the QGP experiments. A reliance on accelerators and detectors automatically enforces talk of sharply localized particles traveling in trajectories. Nevertheless, such a switch is possible in principle. We are using “language game” as a replacement for Bohr’s “phenomenon”. Both are treated holistically as epistemologically irreducible units. As such an account must include the apparatus used. The primordial QGP resulting from the big bang has no machinery to localize particles. It requires a different language game. This allows for the possibility of speaking of quarks in wave rather than particle terms. Quarks, regarded as particles, are assigned a size of 10−17 cm. A rough calculation of the de Broglie wavelengths of quarks traveling at 99% of the speed of light yields the following values expressed in units of 10−17 cm, for different quarks: up 0.5; down 0.25; strange 0.15; charmed 0.012; bottom 0.0035; top 0.00009. These values might yield the localization required without a reliance on particle ontology. However, I have no idea how such an account might be developed.
The experimental approach to interpretation considered here does not yield a fundamental ontology of reality. However, it presupposes a functional ontology and can contribute to advances in ontology. To indicate one way in which this is possible we can adapt the EFT approach to beta decay considered earlier to B meson decay. Besides known decay processes there is a possibility of further decays. Such a decay for the heaviest B meson, Bc, can be symbolically represented in a Feynman diagram.

The black ball signifies possible decays that could include virtual particles much heavier than W and Z mesons. Such particles are predicted by both super-symmetry and higher order gauge theories like SU(6) and SU(10). Replacing the black ball by virtual interactions involving new particles might not tell us what the world is like if, for example, super-symmetry is true of it. But it would advance our knowledge of the future of the world.
Cite this paper
MacKinnon, E. (2017) Experiments and Functional Realism. Open Journal of Microphysics, 7, 67-84. http://dx.doi.org/10.4236/ojm.2017.74005
References
- 1. Hughes, R.I.G. (1989) The Structure and Interpretation of Quantum Mechanics. Harvard University Press, Cambridge.
- 2. Van Fraassen, B. (1991) Quantum Mechanics: An Empiricist View. Clarendon Press, Oxford. https://doi.org/10.1093/0198239807.001.0001
- 3. Gelis, F. (2011) The Early Stages of a High-Energy Heavy Ion Collision. arXiv:1110.1544v1 [hep-ph].
- 4. Lincoln, D. (2009) The Quantum Frontier: The Large Hadron Collider. The Johns Hopkins University Press, Baltimore.
- 5. Aamodt, K., et al. (2011) Charged-Particle Multiplicity Density at Mid-Rapidity in Central Pb-Pb Collisions at Sqrt(SNN = 2.76 Tev). Physical Review Letters, 105, 252301. https://doi.org/10.1103/PhysRevLett.105.252301
- 6. Aggarwal, M.M., et al. (2010) An Experimental Exploration of the QCD Phase Phase Diagram: The Search for the Critical Point and the Onset of Deconfinement. arXiv:1007.2613v1.
- 7. Adams, J., et al. 2005. Experimental and Theoretical Challenges in the Search for the Quark Gluon Plasma: The STAR Collaboration’s Critical Assessment of the Evidence from RHIC Collisions. arXiv:nucl-ex/0501009v3.
- 8. Kolb, P.F. and Heinz, U. (2003) Hydrodynamic Description of Ultrarelativistic Heavy-Ion Collisions. arXiv:nucl-th/0305084.
- 9. Zajac, W.A. (2008) The Fluid Nature of the Quark-Gluon Plasma. arXiv:0802.3552v1 [nucl-ex].
- 10. Iancu, E. and Wu, B. (2015) Thermalization of Mini-Jets in a Quark-Gluon Plasma. Journal of High Energy Physics, 155. arXiv:1512.09353v1 hep-ph, 1-4. https://doi.org/10.1007/JHEP10(2015)155
- 11. Cacciari, M. and Salam, G.P. (2008) The Anti-kt Jet Clustering Algorithm. arXiv:0802.1189v2 [hep-ph].
- 12. Bohr, N. (1963) Essays 1958-1962 on Atomic Physics and Human Knowledge. Wiley, New York.
- 13. Honner, John. 1987a. The Description of Nature: Niels Bohr and the Philosophy of Quantum. Oxford: Clarendon Press.
- 14. MacKinnon, E. (2011) Interpreting Physics: Language and the Classical/Quantum Divide. Springer, Amsterdam.
- 15. Heisenberg, W. (1958) Physics and Philosophy: The Revolution in Modern Science. Harper’s, New York.
- 16. Pauli, W. (1964) Collected Scientific Papers. Interscience, New York.
- 17. Bohm, D. (1952) A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables. Physical Review, 85, 166-193.
- 18. Davisson, C.J. (1928) Are Electrons Waves? Vol. 2, Basic Books Inc., New York, 1144-1165.
- 19. Samios, N. (1997) Early Baryon and Meson Spectroscopy Culminating in the Discovery of the Omega-Minus and Charmed Baryons. In: Hoddeson, L., et al., Eds., The Rise of the Standard Model, Cambridge University Press, Cambridge, 525-541. https://doi.org/10.1017/CBO9780511471094.031
- 20. Johnson, G. (1999) Strange Beauty: Murray Gell-Mann and the Revolution in Twentieth-Century Physics. Alfred A. Knopf, New York.
- 21. Kaku, M. (1993) Quantum Field Theory: A Modern Introduction. Oxford University Press, New York.
- 22. Hoddeson, L., et al. (1997) The Rise of the Standard Model: Particle Physics in the 1960s and 1970s. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511471094
- 23. MacKinnon, E. (2008) The Standard Model as a Philosophical Challenge. Philosophy of Science, 75, 447-457. https://doi.org/10.1086/595864
- 24. Georgi, H. (1993) Effective Field Theory. Annual Review of Nuclear and Particle Science, 43, 209-252. https://doi.org/10.1146/annurev.ns.43.120193.001233
- 25. Manohar, A. (1996) Effective Field Theories.
- 26. Kaplan, D. (2005) Five Lectures on Effective Field Theory.
- 27. Hartmann, S. (2001) Effective Field Theories, Reductionism and Scientific Explanation. Studies in History and Philosophy of Modern Physics, 32B, 267-304. https://doi.org/10.1016/S1355-2198(01)00005-3
- 28. Castellani, E. (2002) Reductionism, Emergence, and Effective Field Theories. Studies in History and Philosophy of Modern Physics B, 33, 251-267. https://doi.org/10.1016/S1355-2198(02)00003-5
- 29. Kane, G. (2000) Super Symmetry. Mass. Perseus Publisher, Cambridge.
- 30. Rohrlich, F. (2001) Cognitive Scientific Realism. Philosophy of Science, 68, 185-202. https://doi.org/10.1086/392872
- 31. Chang, R. (1988) Chemistry. McGraw-Hill, New York.
- 32. Scerri, E. (2000) The Failure of Reduction and How to Resist Disunity of the Sciences. Science and Education, 9, 405-425. https://doi.org/10.1023/A:1008719726538
NOTES
1A summary account of jet production and decay is given in [10] . The different algorithms used in treating jets are evaluated in [11] .
2 [21] , Chap. 11 summarizes the SM. A general account of the development of the SM is given in [22] . The contrast between the SM and more rigorous formulations of quantum field theory is analyzed in [23] .
3 [24] [25] and [26] present general accounts of EFTS. The philosophical significance of EFTs has been treated in [27] and [28] .
4See [31] , pp. 344-389. Scerri [32] presents a philosophical justification of this practice.


