Received 25 June 2016; accepted 1 July 2016; published 4 July 2016

ABSTRACT

The present paper is basically written as a non-apologetic strong defence of the thesis that computation is part and parcel of a physical theory and by no means a mere numerical evaluation of the prediction of a theory which comes towards the end. Various general considerations as well as specific examples are given to illustrate and support our arguments. These examples range from the practical aspect to almost esoteric considerations but at the end, everything converges towards a unity of theory and computation presented in the form of modern fractal logic and transfinite quantum field theory in a Cantorian spacetime. It is true that all our examples are taken from physics but our discussion is applicable in equal measure to a much wider aspect of life.

Keywords:

Fractal Logic, E-Infinity Theory, Cantorian-Fractal Spacetime, P. Erdos, A. Turing Computer, Transfinite Turing Machine, A. Connes Noncommutative Geometry, von Neumann Continuous Geometry, Golden Mean Computer, Pointless Geometry, Fuzzy Sets, Fuzzy Logic

1. Introduction

Mathematical computation aided by number theory [1] - [14] , digital and analogue modern computers [14] - [27] are far more basic to quantum physics and cosmology than most theoretical physicists, including the present Author could usually have thought or imagined most of the time until relatively recently [22] - [39] . There are of course a few notable exceptions reaffirming the rule such as the remarkable French pure and applied mathematician Alain Connes [28] as well as the founding farther of so many branches of pure and applied mathematics, John von Neumann [29] .

In the present work we take theoretical physics, exemplified by E-infinity fractal Cantorian theory [31] - [137] into the relatively new direction of science set in computational space to explore nature as a computation [3] - [5] [15] . This is actually the essence of E-infinity theory [31] - [137] . In turn and to close the circle, the core of E-in- finity theory is a transfinite form of a Turing computer [14] [15] . Finally we will see immediately that the essence of this transfinite Turing machine is a simple golden mean based number system, which is at the heart of nature itself [3] [4] [11] [12] .

Said in a few words, our present work is addressing scientists who love numbers but not only numbers such as P. Erdos and S. Ramanujan [19] [20] . To understand nature we need all the tools we can put our hands on and one cannot afford to dismiss computation as merely the trivial end result of a well understood theory. Computation gives us not only an insight into a theory but can also lead to a theory hiding in fine structure details which we did not even suspect that it existed before seeing the inner wheel of the computation process at work as we hope to show here [1] - [155] .

2. A Golden Mean Based Computation

As is in the meantime well known, E-infinity theory makes extensive use of a golden mean based number system. Consequently we start by introducing two fundamental theorems [11] [12] [30] .

Theorem 1

Any positive integer can be written uniquely as the sum of non-consecutive Fibonacci numbers of the following well known series:

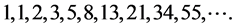
That means the Fibonacci series is given by:

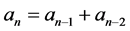
Theorem 2

Any positive real number can be represented uniquely as the sum of non-consecutive number of the following series:

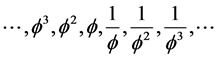
where 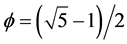is the golden mean which is the ratio of 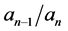for. We discussed the theory and application of this number system as an alternative to traditional and conventional decimal and binary systems in many previous publications [31] - [36] [43] [44] [48] [52] [59] which the reader may consult intermittently as he reads the present paper.

3. What We Ought to Have Learnt from Nonlinear Dynamics and Deterministic Chaos

Deterministic chaos, a phrase coined by American mathematician and pioneer of nonlinear dynamics, chaos and fractal dynamics J. York [138] - [142] , may seem to be a quite contradictory notion. However the message it conveys is very deep indeed and boils down to a peculiar fact, namely that most of what we take to be pure chance is in fact complex and purposeful and yet much of what we know to be a deterministic process is best tackled as if it were pure true randomness. In the light of such philosophy, number theory and some classical books such as that of Hardy [2] as well as the work of P. Erdos [17] [18] and S. Ramanujan [19] [20] became the new holy grail of nonlinear dynamics research [138] - [142] . In addition neither numerical experiments nor number theory were looked down upon, scorned or considered irrelevant to real physics in the relatively new and still vibrant field of deterministic chaos and fractals [137] - [145] [52] - [155] . The Author is rather of the mildly strong opinion that this is a healthy scientific attitude worth exporting from nonlinear dynamics to high energy quantum physics and cosmology [48] [141] and the next sections are concrete examples for what we mean by that.

4. Deriving the Dark Energy and the Ordinary Energy Density of the Cosmos from the Classical Theory of n-Dimensional Spheres

It is important in science to realize the difference between similar things without over estimating either. This is also a lesson from nonlinear dynamics and fractals. There we learnt the crucial difference between a topological dimension and a Hausdorff dimension. Never the less both are dimensions. The marvellous devise Hausdorff dimension [138] [141] on the other hand is closely related not only to the volume of an object but also to its irregularity and consequently it is related to its complexity, entropy [53] and therefore to its surface area, temperature and information. Now we could use this web of interrelationship to give a rather excellent estimation of the dark energy and ordinary energy density of spacetime of the cosmos. Naturally we could not proceed confidently in this way except for the fact that we solved the very same problem using a dozen or more exact methods so that we have considerable knowledge as well as feel and intuition for this problem that many regard as the most fundamental challenge facing modern cosmological research. That is maybe why we cannot hide the feeling of satisfaction and a sense of achievement to be able to give yet another extremely simple solution of this problem using well known and established classical geometry. To do that we need to recall the following facts [143] - [147] .

a) The volume of a 3D, 4D and 5D ball is given by, 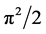and 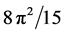respectively.

b) The surface area of a five dimensional sphere is given by.

Now it is obvious that the 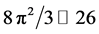of the five dimensional sphere is practically the empty set wave corresponding to the five dimensional cobordism of our four dimensional spacetime. Consequently 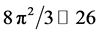may be regarded just as well as the Hausdorff dimension of the cobordism of our 4D spacetime and the five dimensionality as an enveloping Klein-Kaluza spacetime [148] - [150] . Adopting a slightly imaginative mathematical attitude towards the 3D volume of our 3D ball, it can be regarded as the Hausdorff dimensionality of our spacetime which is quite close to its topological dimensionality D = 4 and not far off its E-infinity Hausdorff dimensionality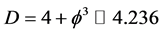. Similarly the volume for five dimensions, i.e. 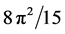may be seen as sufficiently close to the topological dimension of a K-K spacetime, namely five as well as the Hausdorff dimension of the fractal version of K-K [128] [150] , namely. The final result coming out of the above is far simpler than it seems. It is clear that the maximal value of dimensionless pure numbers describing the maximal possible energy must be the larger dimension, i.e. 26 minus the smallest dimension, i.e. 4. On the other hand the next largest possible must be 26 minus 5. It follows then that the largest density under these circumstances must be in the projected ring between D = 5 and D = 4 and is given by the ratio [94] [110] [137]

(1)

Within an integer theory this is the exact value of the dark energy density of the cosmos. Consequently we can interpret the above as follows:

1) The 26 are the largest dimensions of space referred to in mainstream physics as a bosonic spacetime as for instance in the well known heterotic string theory of D. Gross et al.

2) The is clearly the number of compactified extra dimensions where dark energy and dark matter are hiding.

3) The where 25 is the lower critical dimension of the classical Nambu-Goto strings [135] - [137] and the associated Gupta-Bleuler quantization [135] [136] leading to the ghost-free condition a = 1, D = 26 and, where a is the intercept.

Thus we demonstrated that the estimation of based on a classical theory, namely

(2)

is accurate and far from being a coincidence. It is well founded and entails a unity of physics and geometry fused by computation. Needless to say, the above leads naturally to the conclusion that the ordinary energy density corresponding to is and is given by the self explanatory equation [131] - [137]

(3)

4) We could also estimate the dark energy density via the volume of a four and a five dimensional ball. It is quite easy to see that this may be done via the ratio of the two volumes and consequently we have

(4)

which is not far off the exact value. To obtain the exact value we need to introduce transfinite “correction” as frequently done in E-infinity theory by noting that

(5)

and

(6)

The exact value is thus [131] - [137]

(7)

In conclusion of this section we recall that the exact transfinite solution of the problem was based on a dissection of E = mc² of Einstein into two quantum components leading to

(8)

where and. In this dissection the first part is the energy of the quantum particle which is about 4.5% of total energy and since it can be measured it was found that it is nothing but the ordinary energy found by COBE and WMAP cosmological measurements [113] . By contrast the second term is the 95.5% missing energy of the cosmos and is due to the peculiarity of the quantum wave rather than the quantum particle. We will discuss this very same problem in connection with von Neumann-Connes dimensional function [28] [154] in the next section.

5. From von Neumann-Connes Dimensional Function to Physics

Physics-like mathematics is a subject that fascinated and occupied the present Author as a relatively young researcher during his time as a Visiting Professor at Cornell University and later on in Cambridge [21] - [24] [153] . However at that early point of time the Author was not aware of noncommutative geometry as developed and refined by A. Connes [28] building upon von Neumann’s “pointless” continuous geometry [29] [154] . In the end it turned out that the work of A. Connes is closely related to a dimensional function describing the topology of a certain class of Penrose tiling-like manifolds. In turn this dimensional function where and turned out to be completely equivalent to the bijection formula of the Author’s E-infinity theory which states that [125] [154]

(9)

where n is a Menger-Urysohn deductive topological dimension, is the corresponding Hausdorff dimension and is the zero set [31] - [36] .

Let us be explicit in deriving the most important two sets, namely the zero set modelling the pre-quantum particle and the empty set modelling the quantum wave and in the course of doing that lay bare the hidden identity of the dimensional function and the bijection formula. Because it is much easier to work with the bijection formula, we start from there. Setting and inserting in we see that for a Menger-Urysohn topological dimension n = 0, i.e. the zero set we would have the Hausdorff dimension [31] - [36]

(10)

exactly as should be. Next we look at the empty set defined by the inductive Menger-Urysohn topological dimension and inserting again in the bijection formula we find

(11)

Let us see how to reproduce the same result from the dimensional function. It is obvious that to obtain, i.e. to obtain the zero set we must have a = 0 and b = 1 so that one finds the trivial result [28] - [38]

(12)

To find the empty set on the other hand we must have a = 1 and b = −1 from which one finds [28] - [38]

(13)

Now the reader can see for himself that the topological Menger-Urysohn dimension is not immediately obvious from the structure of the dimensional function as it is trivially obvious from the equivalent formalism of the bijection formula. For instance to find D(O) we had to have a = 0 but to find we had to have b = −1. Of course we could define the vital which corresponds to the topological MU dimension as (a) (b) so that for D(O) we find while for we find which is correct and consistent. However it is self evident that this way and although we arrive at the correct result is neither direct nor particularly illuminating. The alternative solution with a dimension function formalism is to stick to the Fibonacci-like recursive nature of the function as indicated at the very beginning. To do that we start best with the following seed and with which we mean [28] - [38]

(14)

and

(15)

Now by subtraction one finds

(16)

and

(17)

We can go on in the same way and find

(18)

and so on as explained in more details elsewhere. Notice that we could go into the “positive” dissection in an analogous way by adding instead of subtracting and find

(19)

and

(20)

and so on. In particular is in the meantime the well known Hausdorff dimension of our quantum- Cantorian spacetime which cannot distinguish between union and intersection because of the unique number theoretical equality

(21)

We can easily see that by inserting the relevant values in the above we find that

(22)

Thus the expectation value of the dimensionality of spacetime is truly unique because

(23)

is indifferent to union and intersection with respect to both the topological dimension where 2 + 2 = (2)(2) = 4 as well as the Hausdorff dimension because

(24)

In this sense our micro-quantum spacetime is truly remarkable from a computational point of view and that is the reason for its “physical” uniqueness which prompts many scientists to ask why are we living in 3 + 1 spacetime?

6. Short Computational and Conceptual Contrast between Quantum Mechanics, String Theory and von Neumann-Connes-E-Infinity Fractal Strings

It is clear that while E-infinity as well as noncommutative geometry are “space manifold” based quantum theories [28] [29] [31] - [33] , orthodox quantum mechanics makes no reference to a spacetime manifold. Many computational consequences result from this fundamental difference [2] - [5] . We discuss this point very briefly and include superstring theory [151] for reasons that will shortly become apparent.

To start with in quantum mechanics we have quantum particles and quantum waves and hardly anything else. However there is no numeric assigned a priori to either a quantum particle or a quantum wave. In string theory we have some definite numbers because the vague point-like particles of quantum mechanics which have no spacetime. We have instead strings with a dimension equal that of a line, namely D = 1. The nearest we come to a fundamental thing resembling a wave in string theory would be the world sheet which has a dimension equal two so that we may start thinking of using two numbers, namely one and two. That way we may regard our 3D space as a string interacting with a world sheet while spacetime is the interaction of two world sheets. Other interpretations are of course possible and were proposed in different forms. This becomes more interesting as we move to E-infinity and von Neumann-Connes fractal strings [28] - [33] . Here we have besides the topological dimensions, a Hausdorff dimension. Thus the counterpart of a D = 1 string is which is the inverse of the Hausdorff dimension of the pre-quantum particle zero set which was replaced by a string in string theory. Numerically it is a string plus a pre-quantum particle giving rise to what we call a fractal string with a Hausdorff dimension equal. Topologically it is however a two dimensional object because of the fact that. As for the fractal object corresponding to the D = 2 world sheet, we have in this case another object with. This may be seen as a fractal string plus one non-fractal string interacting in union to give rise to or simply a pre-quantum particle in union with a classical string world sheet 2 giving rise to what we may call a fractal world sheet . This is clearly a three rather than two dimensional object because . The interesting point is that adopting this fractal string picture we see the time dimension must be fractal in nature because a string plus a world sheet in classical string theory would lead to 1 + 2 = 3 dimensional space but including the fractal fine structure the same sum would give

(25)

which means and this is our fractal spacetime dimensionality [134] .

7. Connectivity Dimension and the Electroweak Energy Scale

The following derivation is yet another example of how mathematics and physics mingle via computation and result in the uncovering of unsuspected interrelations with deep insight and understanding. Let us start from a logarithmic “gauging” of the bijection formula [35] [36]

. (26)

That way one finds [69]

. (27)

Setting n = D_c and and solving for D one finds

. (28)

Now could be taken to be a complexion of an intricate graph and D_c then becomes the well known connectivity dimension of this complex. Setting as our complexion the largest physically known dimensionless number, then it is intuitively obvious that our best bet must be Newton’s dimensionless gravity constant between two protons [69] . Inserting into our D_c one finds a deep meaningful result, namely the inverse electromagnetic constant at the electroweak unification energy scale [69]

(29)

Needless to say is an experimentally well established result in no less measure than of electromagnetism [59] [69] .

8. Erdős Small World Connectivity and String Theory

The legendary Hungarian number theoretician Paul Erdős [17] [18] came close to proving a remarkable theorem about connectivity which when translated to the language of modern social media would mean that it is sufficient to have only 24 acquaintances of each of us to connect almost the entire population of the planet earth. Based on this theorem the Author conjectured that the correct “dimensionality” for this aspect of small world social media must be 26 + k = 26.18033989 which is the bosonic strings fractal dimension [155] . Research in small world science runs in part in a way similar to nonlinear dynamics and chaos [155] and makes extensive use of numerical experiments with little regard for any undue reluctance to indulge in computational mathematics fearing the usual readymade labels, which we need not mention here. Rather than wasting time and space on opposing what is essentially human arrogance produced by ignorance we better discuss next a truly remarkable result of a man of the mold of Paul Erdős [17] [18] taken to the extreme. This man is S. Ramanujan [19] [20] .

9. From Fractal Logic and Cesaro Convergence to the Standard Model of High Energy Physics

The following infinite sum must be one of the most absurd looking results because adding the positive integers from 1 to infinity in the history of mathematics could not in ordinary logic give a negative fraction. It was introduced by the Indian mathematical visionary S. Ramanujan [19] [20] and we can assure the reader that it is not only correct but also has various physical applications in physics including superstrings [151]

(30)

As usual in such situations the apparent absurdity is only apparent and lies in what we really mean with the mathematical symbols. The point is that the result is the Cesaro limit of this otherwise naturally diverging series. We will not discuss the pure mathematics of this highly interesting field but will concentrate on its relation to our fractal logic as employed to counting the messenger particles of the standard model. We may recall that the standard model is based on SU(3), SU(2) and U(1) Lie symmetry groups and that its constant dim (SU(3) SU(2) U(1)) = 12 elementary messenger particles excluding the mass and gravity section which means that it is not complete [152] . Using our fractal logic counting we showed on many earlier occasions that the 12 particles have the weighted number 11.7082033 and means that we have 14 elementary messenger particles [152] . In other words we can write an equality which is not less absurd but in fact more outrageous in its appearance than the sum of Ramanujan [20] introduced earlier on and states that:

(31)

Now let us see if something useful could come out of this systematic madness which is never the less mathematically well founded and we expect that anything that is mathematically founded is logical and in turn it is our metaphysical conviction that it will be used by nature in one way or another. Rearranging one finds from the expression of the Cesaro limit of our series that [151]

(32)

Now all these negative integers could be seen in various different ways. Firs they could be seen as the Menger- Urysohn dimensions with increasing degrees of emptiness. This means we are dealing with the true vacuum considered a multi-fractal of empty set with infinite hierarchal dimensions. Remembering that the expectation value of E-infinity Cantorian-fractal spacetime is the inversion of the dimensionality of the empty set surrounding the quantum wave, i.e. it is the empty set surrounding, we see that the inverse of the vacuum multi-fractal empty set are the exact opposite dimension of finding the expectation value for spacetime such as or in fact Witten’s fractal M-theory [128] . For instance if spacetime is taken as in M- theory as D = 11, then setting a single photon in D = 11 gives us a spacetime of the F-theory type with dimensions [128] . On the other hand in E-infinity theory as well as von Neumann-Connes theory the dimensionality 11 becomes as in the fractal version of M-theory as the photon is given the weighted number rather than unity. Consequently becomes

(33)

where is the exact E-infinity inverse electromagnetic fine structure constant. In other words the fractal logic that is the true logic of counting in high energy physics and cosmology indicates that the fractal number of the elementary messenger bosons are indeed equal not 12 but 11.70820393 and that translated to our normal integer counting this number is 14 which means in turn that we can consider the standard model complete and include the graviton although it is overlooked theoretically for being essentially a fractal fine structure which makes it also even more difficult to detect experimentally than the illusive Higgs [152] .

From the above admittedly complex discussion and somewhat subtle to the degree bordering on terse reasoning, we see that our Cesaro sum is a relative of our theory and we could just interpret 12 as being which is the fractal weight number of 14 elementary messenger particles. This is the reason why we can obtain the exact integer based value of the ordinary and the dark energy density of the cosmos from Witten’s M-theory as [94] [128]

(34)

while the exact transfinite expression is given by Witten’s fractal M-theory as [94] [128]

(35)

In conclusion of this section we may mention on passing a remarkable decomposition of E = mc² into three parts corresponding and agreeing with the actual cosmic measurements of ordinary energy, dark matter and pure dark energy of the cosmos

(36)

where is ‘tHooft’s renormalon and with being Hardy’s entangleon.

10. Discussion

When the great E. Witten set out to construct his acclaimed M-theory he rightly chose to start with the most important invariant of a topology and reasoned that he needed seven spacetime dimensions to embed the Lie symmetry groups of the standard model, i.e. the SU(3) SU(2) U(1). Consequently an optimal spacetime must be the sum of Einstein’s 4 spacetime dimensions plus these seven and so he arrived at the same dimension of super gravity, namely [128]

(37)

Now the Author asks the reader to pay special attention to how our transfinite computational methodology leads almost automatically to the same result and even a little more. First we know that our quantum spacetime most important dimensionality is that of its core, namely which is nothing more than. Next we ask what is the dimensionality of the space that constitutes the boundary of this core? Clearly by an obvious cobordism argument, the boundary space must be given by. Together core space and boundary space amount to the union, i.e. the sum of both dimensions. This means

(38)

This is a remarkable way to reproduce Witten’s famous result, since is a very small value compared to the 4 + 7 = 11. Thus neglected the small irrational tail we find in the original dimensionality of M-theory

(39)

However if we insist upon being pedantically accurate and include the small we are rewarded with a pleasant surprising result, namely that is Hardy’s celebrated probability of quantum entanglement of two quantum particles. In addition the continued fraction of the exact value becomes

(40)

Thus we find a Russian doll-like 11-D Witten spacetime inside another 11-D spacetime and so on indefinitely. The reader may also be intrigued to see that the dimensionality of enveloping space given by is simply and is nothing more than the inverse of Hardy’s quantum entanglement. This is the beginning of discovering the fractal version of Witten’s M-theory and at the same time, the main message of the present paper. At the risk of being a little repetitive, computation is an indispensible part of the theory and not only mere numeric. That is why we see meaning and physics in results that at first glance may seem absurd and

faulty although it is not such as of Ramanujan [19] [20] and the many other results such as our

equation No. 31 reported in the present paper.

11. Conclusion

Computation lies at the root of the very process of thinking. It is not the last stage of a theory but more often than not, it should be at the beginning of theoreticizing. Number systems can help us present a theory in a much simpler way than thought possible and the present Author suspects that nature is basically a kind of gigantic computer of the transfinite golden mean based Turing type. What distinguishes this computer from the classical Turing machine is the software which we allege is based on a transfinite golden mean binary system introduced at the very beginning of the present paper and is therefore virtually infinitely more powerful than any known computer. There are many implicit results and consequences in the present work which we did not mention due to space limitation, for instance the mere fact that shows where the roots of the problem of fine tuning in physics and cosmology lies. We hope to come to these and similar points in the future.

Acknowledgements

This paper is indebted to the work of A. Connes, G. Hardy and S. Ramanujan. It is dedicated to peace in the Middle East and the ideal of a United States of The Middle East, which is a natural demand arising from applying computational fractal logic to a most troubled part of our world.

Cite this paper

Mohamed S. El Naschie, (2016) High Energy Physics and Cosmology as Computation. American Journal of Computational Mathematics,06,185-199. doi: 10.4236/ajcm.2016.63020

References