World Journal of Nuclear Science and Technology
Vol.3 No.1(2013), Article ID:27465,5 pages DOI:10.4236/wjnst.2013.31001
On the Build-Up Factor from the Multi-Group Neutron Diffusion Equation with Cylindrical Symmetry
Department of AppliedMath, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil
Email: julio.lombaldo@ufrgs.br, bado.bodmann@ufrgs.br, vilhena@ufrgs.br, borges@ufrgs.br
Received August 9, 2012; revised October 7, 2012; accepted October 21, 2012
Keywords: Build-Up Factor; Cylindrical Geometry; Hankel Transform
ABSTRACT
We consider the time dependent neutron diffusion equation for one energy group in cylinder coordinates, assuming translational symmetry along the cylinder axis. This problem for a specific energy group is solved analytically applying the Hankel transform in the radial coordinate r. Our special interest rests in the build-up factor for a time dependent linear neutron source aligned with the cylinder axis, which in the limit of zero decay constant reproduces also the static case. The new approach to solve the diffusion equation by integral transform technique is presented and results for several parameter sets and truncation in the solution for the flux and build-up factor are shown and found to be compatible to those of literature [1,2].
1. Introduction
Energy production and environmental issues are strongly related and even though recent events have put nuclear energy on the black list of energy sources, it will recover its role in world’s energy production matrices. In this sense it remains meaningful to search for progress in topics related to nuclear reactor theory, especially by virtue of recent efforts in innovative nuclear reactor technology. As a contribution in this line we develop an analytical method to determine the build-up factor for neutrons, the description of neutron distributions inside the nuclear reactor core. Note, that other applications with this method are possible such as radiation protection, nuclear medicine, among others, see the works [3-5]. The mathematical model that serves as our starting point is motivated by the S2 approximation of the Boltzmann equation, i.e. the diffusion equation [6]. This equation represents the balance between production and loss of these particles, described in the next section. In Sections 2 and 3 we solve this problem in an analytical fashion using the finite Hankel Transform, which is appropriate for problems represented in cylindrical coordinates, following the idea of the solution of this kind of problem in Cartesian geometry [7,8].
2. Neutron Diffusion
We consider the time dependent neutron diffusion equation for one energy group in cylinder coordinates, assuming translational symmetry along the cylinder axis
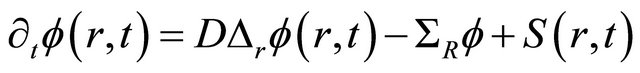 (1)
(1)
Here  is the scalar neutron flux, D is the diffusion coefficient for neutrons,
is the scalar neutron flux, D is the diffusion coefficient for neutrons,  is the radial part of the elliptic operator, given by
is the radial part of the elliptic operator, given by
 (2)
(2)
The  is the macroscopic removal cross section and
is the macroscopic removal cross section and  is the source of the problem, that depends on r and t, respectively. Equation (1) is subject to the following boundary conditions
is the source of the problem, that depends on r and t, respectively. Equation (1) is subject to the following boundary conditions
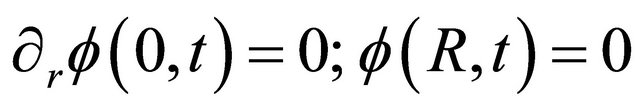 (3)
(3)
This problem for one energy group may be solved analytically applying the Hankel transform in the radial coordinate r in cylindrical geometry.
3. Solution by Finite Hankel Transform
Next, we apply the Finite Hankel transform of order zero to (1), making use of some properties of the transform. Recalling, that the Hankel transform of order p has the definition,
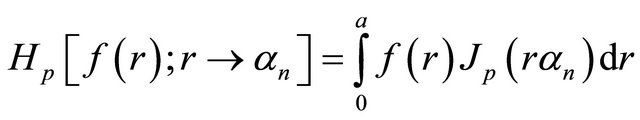 (4)
(4)
where 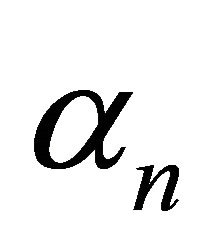 are values such that
are values such that 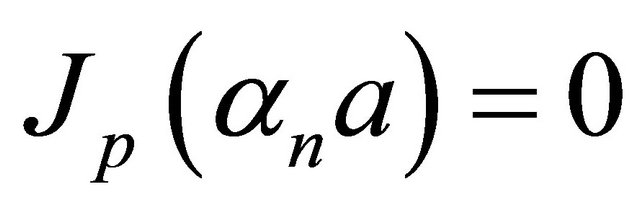 for
for , and the inversion is given by
, and the inversion is given by
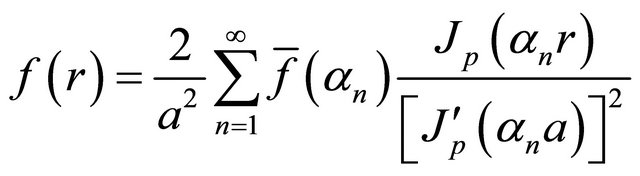 (5)
(5)
Differently, than in other applications, where the transform has an infinite upper limit, here the integral has an upper limit R due to the assumption that the flux outside the cylinder with radius R is zero and especially  holds. Since the neutron flux is related to a distribution means that
holds. Since the neutron flux is related to a distribution means that  is limited. Our special interest is in the build-up factor for the unique initial condition
is limited. Our special interest is in the build-up factor for the unique initial condition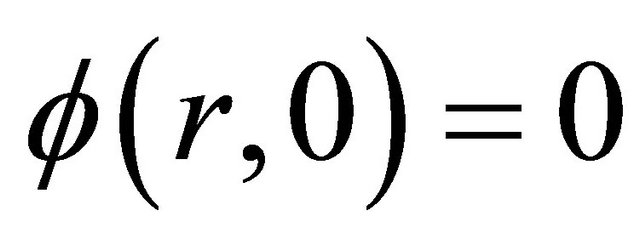 . Upon multiplying both sides of (1) by
. Upon multiplying both sides of (1) by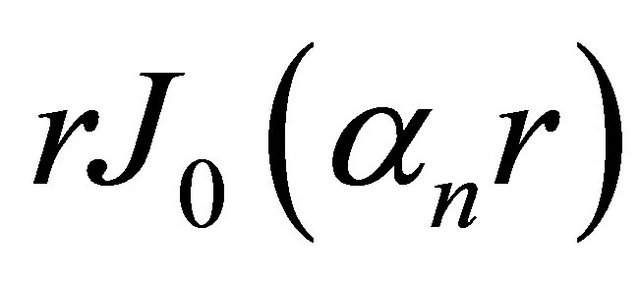 , and integrating from 0 to the radius R, we obtain
, and integrating from 0 to the radius R, we obtain
 (6)
(6)
where 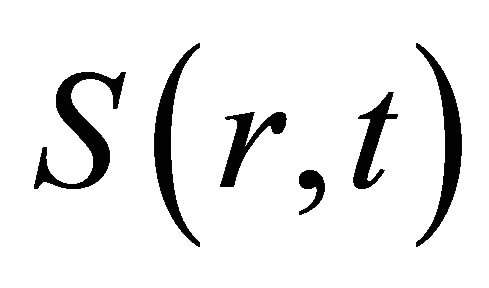 is the source term of the problem. Using the transformed quantities (6) can be rewritten
is the source term of the problem. Using the transformed quantities (6) can be rewritten
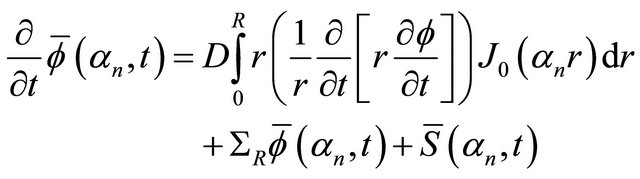 (7)
(7)
The integral containing the spatial derivative may be cast into an expression containing transformed quantities using integration by parts,
 (8)
(8)
which further simplifies due to the choice of 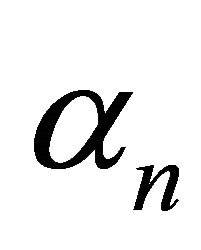 such that
such that 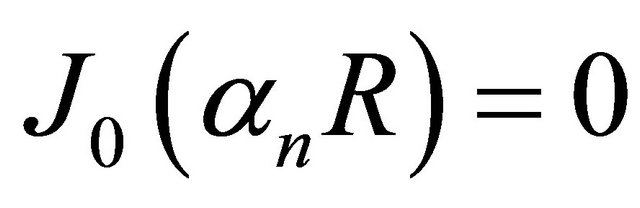 and implies that the first term of the right side in (8) vanishes. Therefore,
and implies that the first term of the right side in (8) vanishes. Therefore,
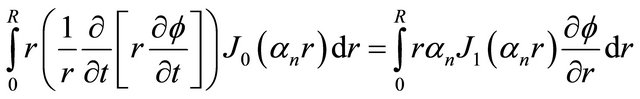 (9)
(9)
which by virtue of
 (10)
(10)
reduces to
 (11)
(11)
This equation is subject to the initial condition 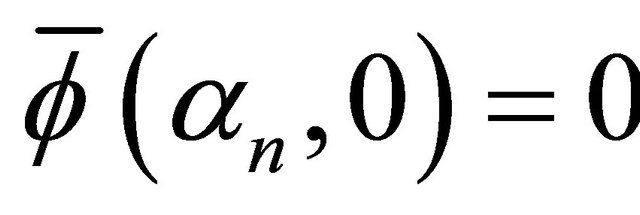 because
because 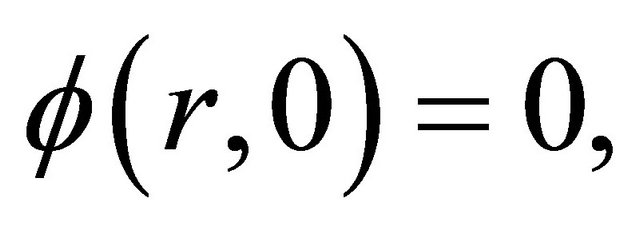 and has the solution,
and has the solution,
 (12)
(12)
with,
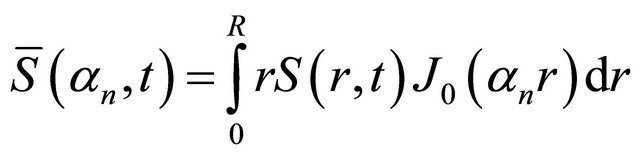 (13)
(13)
The inversion may be obtained by the use of the definition of the inversion (5) applied to Equation (12). Thus, we obtain the result
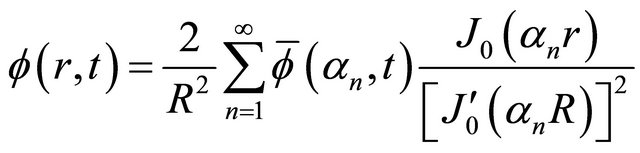 (14)
(14)
and expressed in terms of Equation (12) is
 (15)
(15)
that is the solution for the group g. For example, if we consider a fixed source, in this case, we have a source without time dependence, and the inversion (15), can be written as
 (16)
(16)
with
 (17)
(17)
and therefore, the final expression for the flux is
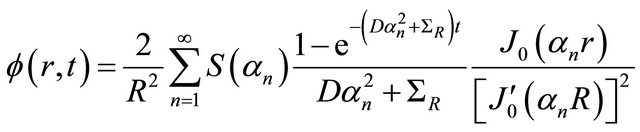 (18)
(18)
4. Infinite Line Source Distribution
We consider now as a source a string that coincides with the centre of the cylinder and may be represented by the Delta Function  (in cylindrical case), which is defined to be zero for all values of r except at r = 0. The integral of
(in cylindrical case), which is defined to be zero for all values of r except at r = 0. The integral of 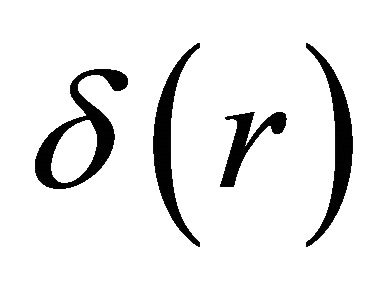 is finite, provided r = 0 lies in the range of integration, and the value of the integral is taken to be unity. In order to treat the special case, where r = 0 lies at the border of the interval we recall, that for any compact set
is finite, provided r = 0 lies in the range of integration, and the value of the integral is taken to be unity. In order to treat the special case, where r = 0 lies at the border of the interval we recall, that for any compact set 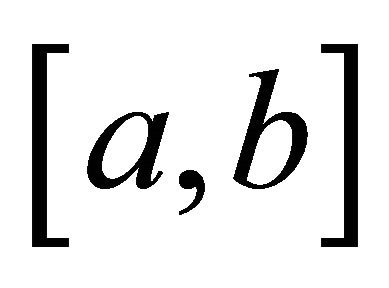 with
with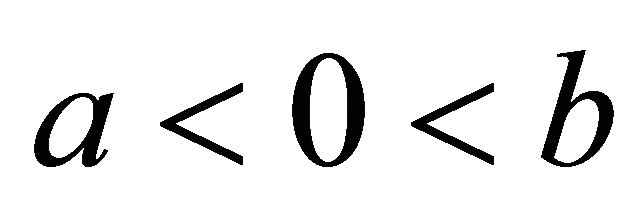 , that is a compact support for
, that is a compact support for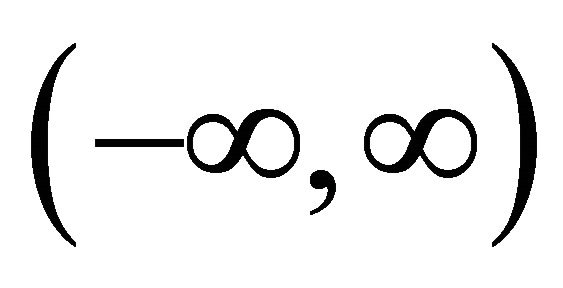 .
.
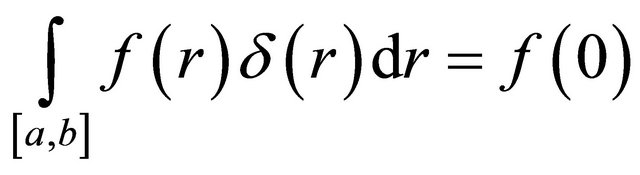 (19)
(19)
holds as usual, since r = 0 lies truly in the interval. In the case where r = 0 lies at the interval limit, the following limit shall be applied to determine the integral property from above.
 (20)
(20)
The Hankel transformed expression for the source as well as in (13). If we have the source has time dependence, as for instance the classical example from reference [9]
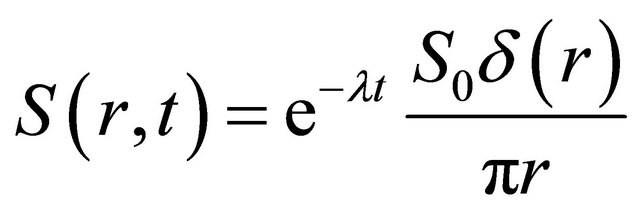 (21)
(21)
where 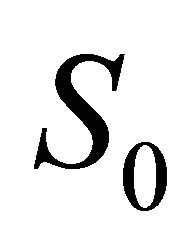 is the initial value for the source, and
is the initial value for the source, and 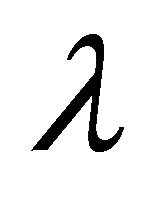 is the decay constant, then for
is the decay constant, then for .
.
 (22)
(22)
Finally, we can express the final solution for the flux, making use of the inversion using (22), yields then
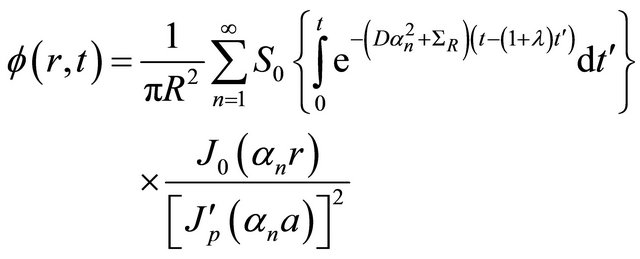 (23)
(23)
The integral in the previous equation may be solved,
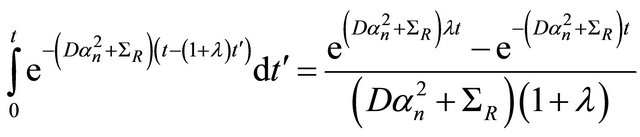 (24)
(24)
so that the final solution reads
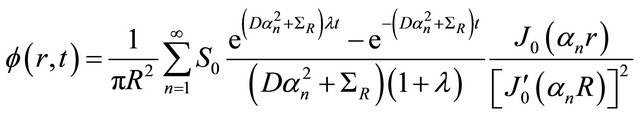 (25)
(25)
The time dependent source solution also includes the time independent source term upon taking the limit .
.
5. Analysis of Build-Up Factor
The build-up factor have been calculated for different response functions that have impact on the design of fuel element distribution. The composition used in this work is that used in the Mirror Advanced Reactor Study (MARS) design. The build-up factor for the response function from an infinite line source is defined as
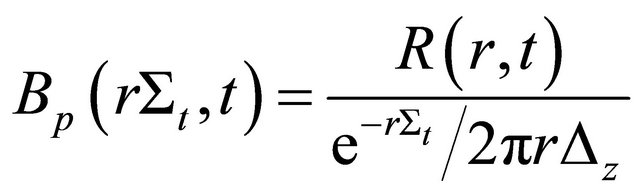 (26)
(26)
where  is a unit height of the cylinder. The use of the unit length along the cylinder axis is necessary, due to the fact that we considered an infinite cylinder. In our case, we will consider the response function being the flux inside the cylinder divided by the decay constant in order to render the build-up factor dimensionless
is a unit height of the cylinder. The use of the unit length along the cylinder axis is necessary, due to the fact that we considered an infinite cylinder. In our case, we will consider the response function being the flux inside the cylinder divided by the decay constant in order to render the build-up factor dimensionless
 (27)
(27)
Here 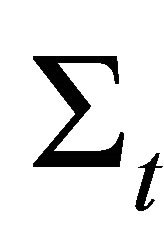 is the total macroscopic cross section. Therefore, the build-up factor in this case in terms of the ratio of the flux including scattering by the flux without scattering is
is the total macroscopic cross section. Therefore, the build-up factor in this case in terms of the ratio of the flux including scattering by the flux without scattering is
 (28)
(28)
As the material thickness increases from zero to a few mean free paths, the energy spectra of neutrons change considerably. Different build-up factors obtained depend on the energy dependence of cross sections for the different response functions. However, after a few mean free paths, the neutron spectra assume fixed shapes. This stems from the fact that the mean free path for a fission source of neutrons is larger than for lower energy neutrons, as thermal neutrons for instance. This results in the same build-up factor variation with the material thickness regardless of the response function. In Figure 1 we show the correlation of the build-up factor with the radius of our cylinder.
6. Results
In this section we present a selection of results for several parameter sets and truncation N = 10 in the solution for the flux and build-up factor. The results are comparable to those from other authors.
The results for the fluxes depending on the parameter choice are shown in Figures 2-5.
7. Conclusion
In this work, we established the existence for the time dependent neutron flux and build-up factor solution of the time dependent neutron diffusion problem in cylindrical geometry using the Hankel transform for a linear source aligned with the cylinder axis. The obtained solution applies to the time dependent case as well as the time independent case if the decay constant is taken in the zero limit. Since existence and uniqueness of the solution

Figure 1. Build-up factor for different values of t.
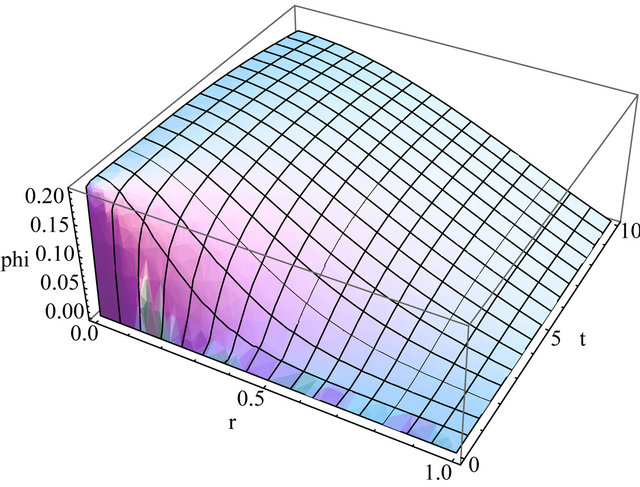
Figure 2. Flux using D = 1.43, ΣR = 0.39, λ = 0.37, t = [0, 10] and truncation at N = 10.

Figure 3. Flux using D = 1.13, ΣR = 0.39, λ = 0.58, t = [0, 10] and truncation at N = 10.
is guaranteed by the Cauchy-Kovalewsky theorem, that includes the present equation as a special case, we showed a new approach to solve the diffusion equation by integral transform technique. This procedure allows

Figure 4. Flux using D = 1.43, ΣR = 0.39, λ = 0.58, t = [0, 30] and truncation at N = 10.
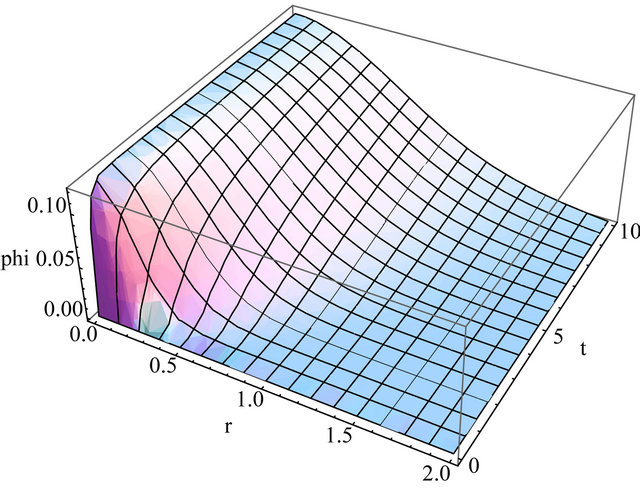
Figure 5. Flux using D = 1.13, ΣR = 0.39, λ = 0.58, t = [0, 10] and truncation at N = 10.
us to generate a function library that efficiently supplies with these solutions, where only the physical and geometrical parameters need to be specified. Furthermore, this method has the advantage, that for numerical purposes the solution may be considered quasi exact, once an adequate number of terms of the solution expansion is taken into account. An error analysis that will specify the truncation index is currently in progress. It is noteworthy, that no numerical errors have to be taken care of due to the analytical character of the solution. Finally motivated by the preliminary good results attained by this methodology, in a forthcoming paper we shall present results for a heterogeneous problem with regions of different physical properties.
8. Acknowledgements
The authors are gratefully to CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) for the partial financial support of this work. A special acknowledgment for the project INCT (Instituto Nacional de Ciencia e Tecnologia-Reatores Nucleares Inovadores) for financial support.
REFERENCES
- J. Wood, “Computational Methods in Reactor Shielding,” Pergamon Press, Oxford, 1982.
- B. D. A. Rodriguez, M. T. Vilhena and V. Borges, “The Determination of the Exposure Build-Up Factor Fomultion in a Slab Using the LTSN Method,” Kerntechnik, Vol. 71, No. 4, 2006, pp. 182-184.
- H. Hirayama and K. Shin, “Application of the EGS4 Monte Carlo Code to a Study of Multilayer Gamma-Ray Exposure Build-Up Factors,” Journal of Nuclear Science and Technology, Vol. 35, No. 11, 1998, pp. 816-829. doi:10.1080/18811248.1998.9733949
- B. D. A. Rodriguez, M. T. Vilhena and V. Borges, “A Solution for the Two-Dimensional Transport Equation for Photons and Electrons in a Rectangular Domain by the Laplace Transform Technique,” International Journal of Nuclear Energy Science and Technology, Vol. 5, No. 1, 2010, pp. 25-40.
- G. C. Pomraning, “Flux-Limited Diffusion and FokkerPlanck Equations,” Nuclear Science and Engineering, Vol. 85, No. 2, 1983, pp. 116-126.
- M. T. Vilhena, C. F. Segatto and L. B. Barichello, “A Particular Solution for the SN Radiative Transfer Problems,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 53, No. 4, 1995, pp. 467-469. doi:10.1016/0022-4073(95)90020-9
- V. Borges, J. C. L. Fernandes, M. T. Vilhena, B. Bodmann and B. D. A. Rodriguez, “A Closed-Form Formulation for the Build-Up Factor and Absorbed for Photons and Electrons in the Compton Energy Range in Cartesian Geometry,” World Journal of Nuclear Science and Technology, Vol. 1, No. 2, 2012, pp. 23-28. doi:10.4236/wjnst.2012.21004
- C. Borges and W. Larsen, “The Transversed Integrated Scalar Flux of a Narrowly Focused Particle Beam,” SIAM Journal on Applied Mathematics, Vol. 55, No. 1, 1995, pp. 1-22.
- J. Lamarsh, “Introduction to Nulcear Reactor Theory,” McGrawn-Hill Company, New York, 1972.

